
【题目】如图,正方形ABCD的边长为a,点E在边AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且![]() ,CF与AD相交于点G,连接EC,EF,EG,则下列结论:①∠ECF=45°;②
,CF与AD相交于点G,连接EC,EF,EG,则下列结论:①∠ECF=45°;②![]() 的周长为
的周长为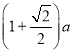 ;③
;③![]() ;④
;④![]() 的面积的最大值
的面积的最大值![]() .其中正确的结论是____.(填写所有正确结论的序号)
.其中正确的结论是____.(填写所有正确结论的序号)
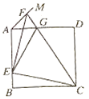
【答案】①④
【解析】
①正确.如图1中,在BC上截取BH=BE,连接EH.证明△FAE≌△EHC(SAS),即可解决问题;
②③错误.如图2中,延长AD到H,使得DH=BE,则△CBE≌△CDH(SAS),再证明△GCE≌△GCH(SAS),即可解决问题;
④正确.设BE=x,则AE=a-x,AF=![]() ,构建二次函数,利用二次函数的性质解决最值问题.
,构建二次函数,利用二次函数的性质解决最值问题.
解:如图1,在BC上截取BH=BE,连接EH.
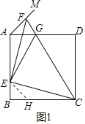
∵BE=BH,∠EBH=90°,
∴EH=![]() BE,∵AF=
BE,∵AF=![]() BE,∴AF=EH,
BE,∴AF=EH,
∵∠DAM=∠EHB=45°,∠BAD=90°,
∴∠FAE=∠EHC=135°,
∵BA=BC,BE=BH,
∴AE=HC,∴△FAE≌△EHC(SAS),
∴EF=EC,∠AEF=∠ECH,
∵∠ECH+∠CEB=90°,∴∠AEF+∠CEB=90°,∴∠FEC=90°,
∴∠ECF=∠EFC=45°,故①正确,
如图2中,延长AD到H,使得DH=BE,则△CBE≌△CDH(SAS),
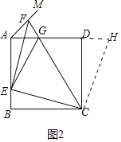
∴∠ECB=∠DCH,∴∠ECH=∠BCD=90°,∴∠ECG=∠GCH=45°,
∵CG=CG,CE=CH,∴△GCE≌△GCH(SAS),∴EG=GH,
∵GH=DG+DH,DH=BE,
∴EG=BE+DG,故③错误,
∴△AEG的周长=AE+EG+AG=AG+GH=AD+DH+AE=AE+EB+AD=AB+AD=2a,故②错误,
设BE=x,则AE=a-x,AF=![]() ,
,
∴∴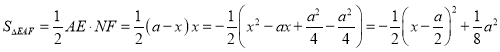 ,
,
∴当![]() 时,
时,![]() 的面积有最大值,最大值是
的面积有最大值,最大值是![]() ,④正确;
,④正确;
故答案为:①④.


科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的外接圆,过点
的外接圆,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() .
.
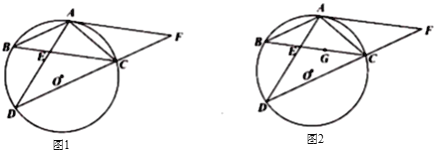
(1)求证:![]() ;
;
(2)求证:![]() 是
是![]() 的切线;
的切线;
(3)如图2,若点![]() 是
是![]() 的内心,
的内心,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,矩形![]() 中,
中,![]() ,点
,点![]() 分别在边
分别在边![]() 上,直线
上,直线![]() 交矩形对角线
交矩形对角线![]() 于点
于点![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处,且点
处,且点![]() 在射线
在射线![]() 上。
上。
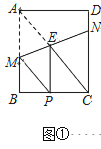

Ⅰ.如图①,当![]() 时,①求证
时,①求证![]() ;②求
;②求![]() 的长;
的长;
Ⅱ.请写出线段![]() 的长的取值范围,及当
的长的取值范围,及当![]() 的长最大时
的长最大时![]() 的长。
的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,O为△ABC内一点.
(1)以O为位似中心,作△A1B1C1,使△A1B1C1与△ABC的相似比为2∶1;
(2)以O为位似中心,作△A2B2C2,使△A2B2C2与△ABC的相似比为1∶2;
(3)若△ABC的周长为12 cm,面积为6cm2,请分别求出△A1B1C1,△A2B2C2的周长和面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
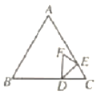
【题目】如图,等边![]() 中,AB=6,点D在BC上,BD=4,点E为边AC上一动点(不与点C重合),
中,AB=6,点D在BC上,BD=4,点E为边AC上一动点(不与点C重合),![]() 关于DE的轴对称图形为
关于DE的轴对称图形为![]() .
.
(1)当点F在AC上时,求证:DF//AB;
(2)设![]() 的面积为S1,
的面积为S1,![]() 的面积为S2,记S=S1-S2,S是否存在最大值?若存在,求出S的最大值;若不存在,请说明理由;
的面积为S2,记S=S1-S2,S是否存在最大值?若存在,求出S的最大值;若不存在,请说明理由;
(3)当B,F,E三点共线时。求AE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
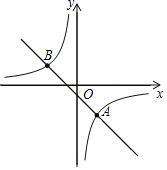
【题目】如图,在平面直角坐标系xOy中,已知直线y=kx+b(k≠0)与双曲线y=![]() (m≠0)交于点A(2,-3)和点B(n,2);
(m≠0)交于点A(2,-3)和点B(n,2);
(1)求直线与双曲线的表达式;
(2)点P是双曲线y=![]() (m≠0)上的点,其横、纵坐标都是整数,过点P作x轴的垂线,交直线AB于点Q,当点P位于点Q下方时,请直接写出点P的坐标.
(m≠0)上的点,其横、纵坐标都是整数,过点P作x轴的垂线,交直线AB于点Q,当点P位于点Q下方时,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线y=-x(x-5)(0≤x≤5),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,若P(2 017,m)是其中某段抛物线上一点,则m为( )
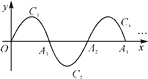
A. 4B. -4C. -6D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
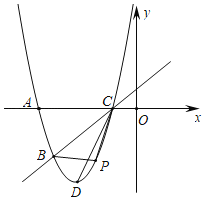
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() 两点,与x轴的另一个交点为C,顶点为D,连结CD.
两点,与x轴的另一个交点为C,顶点为D,连结CD.
(1)求该抛物线的表达式;
(2)点P为该抛物线上一动点(与点B、C不重合),设点P的横坐标为t.
①当点P在直线BC的下方运动时,求![]() 的面积的最大值;
的面积的最大值;
②该抛物线上是否存在点P,使得![]() 若存在,求出所有点P的坐标;若不存在,请说明理由.
若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com