
【题目】如图,在平面直角坐标系xOy中,已知直线y=kx+b(k≠0)与双曲线y=![]() (m≠0)交于点A(2,-3)和点B(n,2);
(m≠0)交于点A(2,-3)和点B(n,2);
(1)求直线与双曲线的表达式;
(2)点P是双曲线y=![]() (m≠0)上的点,其横、纵坐标都是整数,过点P作x轴的垂线,交直线AB于点Q,当点P位于点Q下方时,请直接写出点P的坐标.
(m≠0)上的点,其横、纵坐标都是整数,过点P作x轴的垂线,交直线AB于点Q,当点P位于点Q下方时,请直接写出点P的坐标.
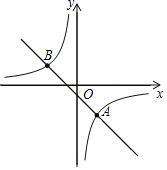
【答案】(1) 反比例函数的解析式为y=-![]() ,一次函数的解析式为y=-x-1.(2) (-6,1)或(1,-6).
,一次函数的解析式为y=-x-1.(2) (-6,1)或(1,-6).
【解析】
(1)利用待定系数法即可解决问题.
(2)由题意点P在点B的左侧或在y轴的右侧点A的左侧,再根据点P的横坐标与纵坐标为整数,即可确定点P坐标.
(1)双曲线y=![]() (m≠0)经过点A(2,-3),
(m≠0)经过点A(2,-3),
∴m=-6,
∴反比例函数的解析式为y=-![]() ,
,
∵B(n,2)在y=-![]() 上,
上,
∴n=-3,
∴B(-3,2),
则有:![]() ,
,
解得:![]() ,
,
∴一次函数的解析式为y=-x-1;
(2)由题意点P在点B的左侧或在y轴的右侧点A的左侧,
∵点P的横坐标与纵坐标为整数,
∴满足条件点点P坐标为(-6,1)或(1,-6).


科目:初中数学 来源: 题型:
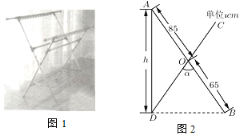
【题目】有一种落地晾衣架如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整晾衣杆的高度. 图2是支撑杆的平面示意图,AB和CD分别是两根不同长度的支撑杆,夹角∠BOD=![]() . 若AO=85cm,BO=DO=65cm. 问: 当
. 若AO=85cm,BO=DO=65cm. 问: 当![]() ,较长支撑杆的端点
,较长支撑杆的端点![]() 离地面的高度
离地面的高度![]() 约为_____
约为_____![]() .(参考数据:
.(参考数据:![]()
![]() ,
,![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组![]() 请结合题意填空,完成本题的解答、
请结合题意填空,完成本题的解答、
(I)解不等式①,得
(II)解不等式②,得
(III)把不等式①和②的解集在数轴上表示出来:
![]()
(IV)原不等式组的解集为
查看答案和解析>>
科目:初中数学 来源: 题型:
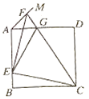
【题目】如图,正方形ABCD的边长为a,点E在边AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且![]() ,CF与AD相交于点G,连接EC,EF,EG,则下列结论:①∠ECF=45°;②
,CF与AD相交于点G,连接EC,EF,EG,则下列结论:①∠ECF=45°;②![]() 的周长为
的周长为 ;③
;③![]() ;④
;④![]() 的面积的最大值
的面积的最大值![]() .其中正确的结论是____.(填写所有正确结论的序号)
.其中正确的结论是____.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仙桃是遂宁市某地的特色时令水果.仙桃一上市,水果店的老板用2400元购进一批仙桃,很快售完;老板又用3700元购进第二批仙桃,所购件数是第一批的![]() 倍,但进价比第一批每件多了5元.
倍,但进价比第一批每件多了5元.
(1)第一批仙桃每件进价是多少元?
(2)老板以每件225元的价格销售第二批仙桃,售出80%后,为了尽快售完,剩下的决定打折促销.要使得第二批仙桃的销售利润不少于440元,剩余的仙桃每件售价至少打几折?(利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出以下命题:
①平分弦的直径垂直于这条弦;
②已知点![]() 、
、![]() 、
、![]() 均在反比例函数
均在反比例函数![]() 的图象上,则
的图象上,则![]() ;
;
③若关于x的不等式组![]() 无解,则
无解,则![]() ;
;
④将点![]() 向左平移3个单位到点
向左平移3个单位到点![]() ,再将
,再将![]() 绕原点逆时针旋转90°到点
绕原点逆时针旋转90°到点![]() ,则
,则![]() 的坐标为
的坐标为![]() .
.
其中所有真命题的序号是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“扶贫攻坚”活动中,某单位计划选购甲、乙两种物品慰问贫困户.已知甲物品的单价比乙物品的单价高10元,若用500元单独购买甲物品与450元单独购买乙物品的数量相同.
①请问甲、乙两种物品的单价各为多少?
②如果该单位计划购买甲、乙两种物品共55件,总费用不少于5000元且不超过5050元,通过计算得出共有几种选购方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
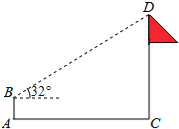
【题目】 如图,在教学实践课中,小明为了测量学校旗杆CD的高度,在地面A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,AC=22米,求旗杆CD的高度.(结果精确到0.1米.参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰Rt△ACB,∠ACB=90°,AC=BC,点A、C分别在x轴、y轴的正半轴上.

(1)如图1,求证:∠BCO=∠CAO
(2)如图2,若OA=5,OC=2,求B点的坐标
(3)如图3,点C(0,3),Q、A两点均在x轴上,且S△CQA=18.分别以AC、CQ为腰在第一、第二象限作等腰Rt△CAN、等腰Rt△QCM,连接MN交y轴于P点,OP的长度是否发生改变?若不变,求出OP的值;若变化,求OP的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com