
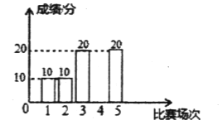
【题目】冰雪之王总决赛(以下简称“雪合战”)在我市落下帷幕.已知不同小组的甲、乙两队的五次预选赛成绩分别如下列不完整的统计表及统计图所示(每次比赛的成绩为0分,10分,20分三种情况).
甲队五次预选赛成绩统计表
比赛场次 | 1 | 2 | 3 | 4 | 5 |
成绩(分) | 20 | 0 | 20 |
| 20 |
已知甲、乙两队五次预选赛成绩的众数相同,平均数也相同.
(1)补全条形统计图;
(2)求甲队成绩的平均数及![]() 的值;
的值;
(3)从甲、乙两队前3次比赛中随机各选一场比赛的成绩进行比较,求选择到的甲队成绩优于乙队成绩的概率.
乙队五次预选赛成绩条形统计图
【答案】(1)见解析(2)20(3)![]()
【解析】
(1)由甲、乙两队五次预选赛成绩的众数相同,且甲队成绩的众数为20可得乙第4场的成绩为20,据此可补全图形;
(2)先计算出乙的平均成绩,据此可得甲的平均成绩,再根据平均数的公式列出关于x的方程,解之可得;
(3)列表得出所有等可能结果,从中找到甲队成绩优于乙队成绩的结果数,利用概率公式计算可得.
(1)![]() 甲、乙两队五次预选赛成绩的众数相同,且甲队成绩的众数为20,
甲、乙两队五次预选赛成绩的众数相同,且甲队成绩的众数为20,
![]() 乙队成绩的众数为20,则第4场的成绩为20,
乙队成绩的众数为20,则第4场的成绩为20,
补全图像如下:
乙队五次预选赛成绩条形统计图
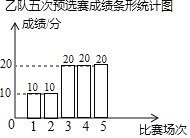
(2)乙队五次成绩的平均数为![]() ,
,
![]() 甲队成绩的平均数为16,
甲队成绩的平均数为16,
由![]() 可得
可得![]() ;
;
(3)列表如下:
10 | 10 | 20 | |
20 | (10,20) | (10,20) | (20,20) |
0 | (10,0) | (10,0) | (20,0) |
20 | (10,20) | (10,20) | (20,20) |
由表可知,共有9种等可能结果,其中甲队成绩优于乙队成绩的情况有4种.
所以选择到的甲队成绩优于乙队成绩的概率为![]() .
.


科目:初中数学 来源: 题型:
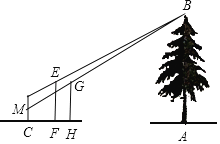
【题目】如图,小华和小康想用标杆来测量河对岸的树AB的高,两人在确保无安全隐患的情况下,小康在F处竖立了一根标杆EF,小华走到C处时,站立在C处看到标杆顶端E和树的顶端B在一条直线上,此时测得小华的眼睛到地面的距离DC=16米;然后,小华在C处蹲下,小康平移标杆到H处时,小华恰好看到标杆顶端G和树的顶端B在一条直线上,此时测得小华的眼睛到地面的距离MC=0.8米.已知EF=GH=2.4米,CF=2米,FH=1.6米,点C、F、H、A在一条直线上,点M在CD上,CD⊥AC,EF⊥AC,CH⊥AC,AB⊥AC,根据以上测量过程及测量数据,请你求出树AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
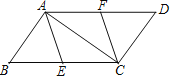
【题目】已知点E、F分别是ABCD的边BC、AD的中点.
(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90°,求AECF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,
中,![]() 为坐标原点,点
为坐标原点,点![]() ,点
,点![]() ,
,![]() 的中线
的中线![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]() 经过
经过![]() ,
,![]() ,
,![]() 三点.
三点.

(1)求圆心![]() 的坐标;
的坐标;
(2)若直线![]() 与
与![]() 相切于点
相切于点![]() ,交
,交![]() 轴于点
轴于点![]() ,求直线
,求直线![]() 的函数表达式;
的函数表达式;
(3)在过点![]() 且以圆心
且以圆心![]() 为顶点的抛物线上有一动点
为顶点的抛物线上有一动点![]() ,过点
,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() .若以
.若以![]() 为半径的
为半径的![]() 与直线
与直线![]() 相交于另一点
相交于另一点![]() .当
.当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里装有2个红球1个黄球,这3个小球除颜色不同外,其它都相同,贝贝同学摸出一个球后放回口袋再摸一个;莹莹同学一次摸2个球,两人分别记录下小球的颜色,关于两人摸到1个红球1个黄球和2个红球的概率的描述中,正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加![]() 元,每天售出
元,每天售出![]() 件.
件.
(1)请写出![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当![]() 为多少时,超市每天销售这种玩具可获利润2250元?
为多少时,超市每天销售这种玩具可获利润2250元?
(3)设超市每天销售这种玩具可获利![]() 元,当
元,当![]() 为多少时
为多少时![]() 最大,最大值是多少?
最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节能减排,我市某校准备购买某种品牌的节能灯,已知3只A型节能灯和5只B型节能灯共需50元,2只A型节能灯和3只B型节能灯共需31元.
(1)求1只A型节能灯和1只B型节能灯的售价各是多少元?
(2)学校准备购买这两种型号的节能灯共200只,要求A型节能灯的数量不超过B型节能灯的数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,O为坐标原点,点A(4,0),以OA为对角线作正方形ABOC,若将抛物线y=![]() x2沿射线OC平移得到新抛物线y=
x2沿射线OC平移得到新抛物线y=![]() (x-m)2+k(m>0).则当新抛物线与正方形的边AB有公共点时,m的值一定是( )
(x-m)2+k(m>0).则当新抛物线与正方形的边AB有公共点时,m的值一定是( )
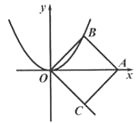
A. 2,6,8B. 0<m≤6C. 0<m≤8D. 0<m≤2或 6 ≤ m≤8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com