Question

13．△ABC中，两边AB和AC的垂直平分线分别与边BC相交于点D和点E，且满足∠BAC+∠DAE=120°，则∠BAC=100°．

Answer 1

分析 设∠BAC=x，根据三角形内角和定理用x表示出∠B+∠C，根据线段的垂直平分线的性质得到DA=DB，EA=EC，根据等腰三角形的性质得到∠DAB=∠B，∠EAC=∠C，根据题意列出方程，解方程即可．

解答 解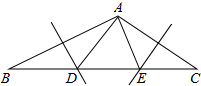：设∠BAC=x，
则∠B+∠C=180°-x，
∵AB和AC的垂直平分线分别与边BC相交于点D和点E，
∴DA=DB，EA=EC，
∴∠DAB=∠B，∠EAC=∠C，
∴∠DAB+∠EAC=180°-x，
∴x-（180°-x）=120°-x，
x=100°，
故答案为：100°．

点评 此题主要考查线段的垂直平分线的性质等几何知识．线段的垂直平分线上的点到线段的两个端点的距离相等．