
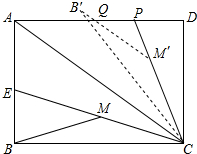
 已知矩形ABCD中,AB=3,BC=4,CE平分∠ACB交AB于点E,M为CE的中点,连结BM,将△BCM绕点C顺时针旋转至△B′CM′,B′M′交AD于Q,延长CM′交AD于P,若PQ=PM′,则PQ=$\frac{25}{8}$-$\frac{2\sqrt{10}}{3}$.
已知矩形ABCD中,AB=3,BC=4,CE平分∠ACB交AB于点E,M为CE的中点,连结BM,将△BCM绕点C顺时针旋转至△B′CM′,B′M′交AD于Q,延长CM′交AD于P,若PQ=PM′,则PQ=$\frac{25}{8}$-$\frac{2\sqrt{10}}{3}$. 分析 首先证明四边形ACM'Q是等腰梯形,设PQ=x,在直角△CDP中,根据勾股定理即可得到关于x的方程求得x的值.
解答 解:设PQ=x,
∵CE平分∠ACB,
∴∠BCE=∠ACE,且$\frac{BE}{AE}$=$\frac{BC}{AC}$,
∵AB=3,BC=4,
∴AC=5,
∴$\frac{BE}{AE}=\frac{4}{5}$,
∴BE=$\frac{4}{3}$,AE=$\frac{5}{3}$,
∴CE=$\frac{4\sqrt{10}}{3}$,
∴CM=$\frac{2\sqrt{10}}{3}$.
∵M是CE的中点,且△BCE是直角三角形,
∴BM=CM=EM,
∴∠CBM=∠BCM=∠ACE,
又△B'CM'是△BCM旋转得到,
∴△B'CM'≌△BCM.
∵PQ=P'M,
∴∠PM'Q=∠PQM'=2∠B'CM'=∠ACB.
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ACB=∠CAD,
∴∠PQM'=CAD,
∴AC∥B'M',
∴∠PM'Q=∠ACP,
∴∠CAD=∠ACP,
∴四边形ACM'Q是等腰梯形,
∴AQ=CM'=$\frac{2\sqrt{10}}{3}$,
∴PD=$\frac{2\sqrt{10}}{3}$+x,
在直角△CDP中,根据勾股定理得:CP2=PD2+CD2,
($\frac{2\sqrt{10}}{3}$+x)2=(4-$\frac{2\sqrt{10}}{3}$-x)2+9,另t=$\frac{2\sqrt{10}}{3}$+x,则t2=(4-t)2+9,
∴t=$\frac{25}{8}$,
∴$\frac{2\sqrt{10}}{3}$+x=$\frac{25}{8}$,
∴x=$\frac{25}{8}$-$\frac{2\sqrt{10}}{3}$,
∴PQ=$\frac{25}{8}$-$\frac{2\sqrt{10}}{3}$.
故答案是:$\frac{25}{8}$-$\frac{2\sqrt{10}}{3}$.
点评 本题考查了图形的旋转,以及等腰梯形的证明和勾股定理的应用,证明四边形ACM'Q是等腰梯形是本题的关键.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
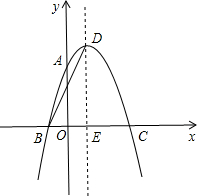 如图,抛物线y=ax2+2x+c经过点A(0,3)、B(-1,0),请解答下列问题:
如图,抛物线y=ax2+2x+c经过点A(0,3)、B(-1,0),请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{3}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com