
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE,BE,BE⊥AE,延长AE交BC的延长线于点F.求证: 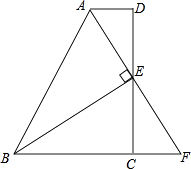
(1)FC=AD;
(2)AB=BC+AD.
【答案】
(1)证明:∵AD∥BC(已知),
∴∠ADC=∠ECF(两直线平行,内错角相等),
∵E是CD的中点(已知),
∴DE=EC(中点的定义).
∵在△ADE与△FCE中,
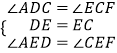 ,
,
∴△ADE≌△FCE(ASA),
∴FC=AD(全等三角形的性质)
(2)证明:∵△ADE≌△FCE,
∴AE=EF,AD=CF(全等三角形的对应边相等),
∴BE是线段AF的垂直平分线,
∴AB=BF=BC+CF,
∵AD=CF(已证),
∴AB=BC+AD(等量代换)
【解析】(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可求出△ADE≌△FCE,根据全等三角形的性质即可解答.(2)根据线段垂直平分线的性质判断出AB=BF即可.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了绿化环境,育英中学八年级三班同学都积极参加植树活动,今年植树节时,该班同学植树情况的部分数据如图所示,请根据统计图信息,回答下列问题:
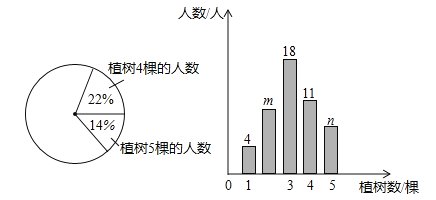
(1)八年级三班共有多少名同学?
(2)条形统计图中,m= ,n= .
(3)扇形统计图中,试计算植树2棵的人数所对应的扇形圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列四个命题:
①经过三个点一定可以作圆;
②等弧所对的圆周角相等;
③三角形的外心到三角形各顶点的距离都相等;
④在同圆中,平分弦的直径一定垂直于这条弦.
其中正确的有()
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E为等腰△ABC的底边BC上一动点,过E作EF⊥BC交AB于D,交CA的延长线于F,问: 
(1)∠F与∠ADF的关系怎样?说明理由;
(2)若E在BC延长线上,其余条件不变,上题的结论是否成立?若不成立,说明理由;若成立,画出图形并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=![]() (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=a(x﹣1)2+c与x轴交于点A( ![]() ,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P′(1,3)处.
,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P′(1,3)处. 
(1)求原抛物线的解析式;
(2)学校举行班徽设计比赛,九年级5班的小明在解答此题时顿生灵感:过点P′作x轴的平行线交抛物线于C,D两点,将翻折后得到的新图象在直线CD以上的部分去掉,设计成一个“W”型的班徽,“5”的拼音开头字母为W,“W”图案似大鹏展翅,寓意深远;而且小明通过计算惊奇的发现这个“W”图案的高与宽(CD)的比非常接近黄金分割比 ![]() (约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据:
(约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据: ![]() ,
, ![]() ,结果可保留根号)
,结果可保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com