
 如图所示,线段AP上有两点M、N,AM:MP=5:11,AN:NP=5:7,MN=2.5,则AP长度是24.
如图所示,线段AP上有两点M、N,AM:MP=5:11,AN:NP=5:7,MN=2.5,则AP长度是24. 科目:初中数学 来源: 题型:填空题
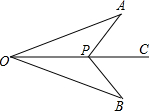 如图,点P是∠AOB的角平分线OC上一点,分别连接AP、BP,若再添加一个条件即可判定△AOP≌△BPO,则一下条件中:①∠A=∠B;②∠APO=∠BPO;③∠APC=∠BPC; ④AP=BP;⑤OA=OB.其中一定正确的是①②③⑤(只需填序号即可)
如图,点P是∠AOB的角平分线OC上一点,分别连接AP、BP,若再添加一个条件即可判定△AOP≌△BPO,则一下条件中:①∠A=∠B;②∠APO=∠BPO;③∠APC=∠BPC; ④AP=BP;⑤OA=OB.其中一定正确的是①②③⑤(只需填序号即可)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 抽取的足球数 | 50 | 100 | 200 | 500 | 1000 | 2000 |
| 优等品数 | 47 | 95 | 194 | 472 | 953 | 1902 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
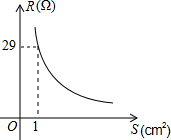 实验表明,当导线的长度一定时,导线的电阻与它的横截面积成反比例,一条长为100km的铅导线的电阻R(Ω)与它的横截面积S(cm2)的函数图象如图所示,那么,其函数关系式为R=$\frac{29}{S}$;当S=2cm2时,R=14.5Ω.
实验表明,当导线的长度一定时,导线的电阻与它的横截面积成反比例,一条长为100km的铅导线的电阻R(Ω)与它的横截面积S(cm2)的函数图象如图所示,那么,其函数关系式为R=$\frac{29}{S}$;当S=2cm2时,R=14.5Ω.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com