
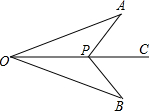
 如图,点P是∠AOB的角平分线OC上一点,分别连接AP、BP,若再添加一个条件即可判定△AOP≌△BPO,则一下条件中:①∠A=∠B;②∠APO=∠BPO;③∠APC=∠BPC; ④AP=BP;⑤OA=OB.其中一定正确的是①②③⑤(只需填序号即可)
如图,点P是∠AOB的角平分线OC上一点,分别连接AP、BP,若再添加一个条件即可判定△AOP≌△BPO,则一下条件中:①∠A=∠B;②∠APO=∠BPO;③∠APC=∠BPC; ④AP=BP;⑤OA=OB.其中一定正确的是①②③⑤(只需填序号即可) 分析 根据全等三角形的判定定理SSS、SAS、ASA、AAS、HL分别进行分析即可.
解答 解:∵点P是∠AOB的角平分线OC上一点,
∴∠AOP=∠BOP,
添加①∠A=∠B,再加上公共边OP=OP可利用AAS判定△AOP≌△BPO;
添加②∠APO=∠BPO,再加上公共边OP=OP可利用ASA判定△AOP≌△BPO;
添加③∠APC=∠BPC可得∠APO=∠BPO,再加上公共边OP=OP可利用ASA判定△AOP≌△BPO;
添加④AP=BP,再加上公共边OP=OP不能判定△AOP≌△BPO;
添加⑤OA=OB,再加上公共边OP=OP可利用SAS判定△AOP≌△BPO;
故答案为:①②③⑤.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a-2)2-4=0 | B. | (a+2)2-5=0 | C. | (a+2)2-3=0 | D. | (a-2)2-5=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | b2=c2-a2 | B. | a2=c2-b2 | C. | b2=a2-c2 | D. | c2=a2+b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com