
【题目】数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为a、宽为b的长方形.用A种纸片- -张,B种纸片一张,C种纸片两张可拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积(答案直接填写到题中横线上);
方法1_________________;
方法2______________________.
(2)观察图2,请你直接写出下列三个代数式: (a+b)2, a2+b2, ab之间的等量关系;
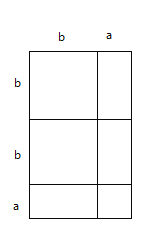
(3)类似的,请你用图1中的三种纸片拼一个图形验证: (a+b)(a+2b)=a2 + 3ab+2b2,请你将该示意图画在答题卡上;
(4)根据(2)题中的等量关系,解决如下问题:
①已知: a+b=5,a2+b2=11, 求ab的值:
②已知(x- 2018)2 +(x- 2020)2=34,求(x- 2019)2的值,

【答案】(1)a2+b2+2ab;(a+b)2;(2)(a+b)2=a2+2ab+b2;(3)见解析(4)①ab=7;②(x-2019)2=16
【解析】
(1)根据正方形的面积求法与割补法即可求解;
(2)根据完全平方公式即可求解;
(3)根据多项式的乘法即可画图;
(4)①根据完全平方公式的变形即可求解;②令x-2019=a,根据完全平方公式即可求解.
(1)图2大正方形的面积
方法一:a2+b2+2ab
方法二:(a+b)2;
(2)(a+b)2, a2+b2, ab之间的等量关系为(a+b)2=a2+2ab+b2;
(3)如图:(a+b)(a+2b)=a2 + 3ab+2b2,
(4)①∵a+b=5,a2+b2=11,
∴(a+b)2= a2+b2+2ab=25
即11+2ab=25,解得ab=7
②(x- 2018)2 +(x- 2020)2=34,
令x-2019=a,
故(a+1)2 +( a-1)2=34,
化简得2a2+2=34
∴a2=16
即(x-2019)2=16


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】某商场有A、B两种商品,每件的进价分别为15元、35元.商场销售5件A商品和2件B商品,可获得利润45元;销售8件A商品和4件B商品,可获得利润80元.
(1)求A、B两种商品的销售单价;
(2)如果该商场计划购进A、B两种商品共80件,用于进货资金最多投入2 000元,但又要确保获利至少590元,请问有那几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图象与一次函数y=mx+b的图象交于A(1,3),B(n,-1)两点.
的图象与一次函数y=mx+b的图象交于A(1,3),B(n,-1)两点.
(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当x取何值时,反比例函数的值大于一次函数的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
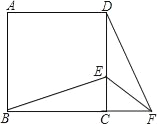
【题目】如图,正方形ABCD中,E为CD边上一点,F为BC延长线上一点,CE=CF.
(1)求证:△BCE≌△DCF;
(2)若∠BEC=60°,求∠EFD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD 边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有( )

A. 4次 B. 3次 C. 2次 D. 1次
查看答案和解析>>
科目:初中数学 来源: 题型:
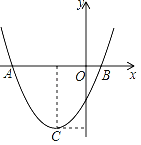
【题目】已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=﹣1,P1(x1,y1)、P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且﹣1<x1<x2,x3<﹣1,则y1、y2、y3的大小关系为( )

A. y1<y2<y3 B. y3<y1<y2 C. y3<y2<y1 D. y2<y1<y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:善于思考的小明在解方程组![]() 时,采用了一种“整体代换”的解法,解法如下:
时,采用了一种“整体代换”的解法,解法如下:
解:将方程②8x+20y+2y=10,变形为 2(4x+10y)+2y=10③,把方程①代入③得,2×6+2y=10,则 y=﹣1;把 y=﹣1 代入①得,x=4,所以方程组的解为:![]() 请你解决以下问题:
请你解决以下问题:
(1)试用小明的“整体代换”的方法解方程组![]()
(2)已知 x、y、z,满足![]() 试求 z 的值.
试求 z 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点C的坐标为(﹣1,﹣3),与x轴交于A(﹣3,0)、B(1,0),根据图象回答下列问题:
(1)写出方程ax2+bx+c=0的根;
(2)写出不等式ax2+bx+c>0的解集;
(3)若方程ax2+bx+c=k有实数根,写出实数k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°,![]() ,则下列结论:①∠CAD=30° ②
,则下列结论:①∠CAD=30° ②![]() ③S平行四边形ABCD=ABAC ④
③S平行四边形ABCD=ABAC ④![]() ,正确的个数是( )
,正确的个数是( )

A.1 B.2 C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com