
【题目】如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°,![]() ,则下列结论:①∠CAD=30° ②
,则下列结论:①∠CAD=30° ②![]() ③S平行四边形ABCD=ABAC ④
③S平行四边形ABCD=ABAC ④![]() ,正确的个数是( )
,正确的个数是( )

A.1 B.2 C.3D.4
【答案】D
【解析】
①先根据角平分线和平行四边形性质得:∠BAE=∠BEA,则AB=BE=1,由有一个角是60度的等腰三角形是等边三角形得:△ABE是等边三角形,由外角的性质和等腰三角形的性质得:∠ACE=30°,最后由平行线的性质可作判断;
②先根据三角形中位线定理得:OE=![]() AB=
AB=![]() ,OE∥AB,根据勾股定理计算OC=
,OE∥AB,根据勾股定理计算OC=![]() 和OD的长,可得BD的长;
和OD的长,可得BD的长;
③因为∠BAC=90°,根据平行四边形的面积公式可作判断;
④根据三角形中位线定理可作判断.
①∵AE平分∠BAD,
∴∠BAE=∠DAE,
∵四边形ABCD是平行四边形,
∴AD∥BC,∠ABC=∠ADC=60°,
∴∠DAE=∠BEA,
∴∠BAE=∠BEA,
∴AB=BE=1,
∴△ABE是等边三角形,
∴AE=BE=1,
∵BC=2,
∴EC=1,
∴AE=EC,
∴∠EAC=∠ACE,
∵∠AEB=∠EAC+∠ACE=60°,
∴∠ACE=30°,
∵AD∥BC,
∴∠CAD=∠ACE=30°,
故①正确;
②∵BE=EC,OA=OC,
∴OE=![]() AB=
AB=![]() ,OE∥AB,
,OE∥AB,
∴∠EOC=∠BAC=60°+30°=90°,Rt△EOC中,OC=![]() =
=![]() ,
,
∵四边形ABCD是平行四边形,
∴∠BCD=∠BAD=120°,
∴∠ACB=30°,
∴∠ACD=90°,
Rt△OCD中,OD=![]() =
=![]() ,
,
∴BD=2OD=![]() ,
,
故②正确;
③由②知:∠BAC=90°,
∴SABCD=ABAC,
故③正确;
④由②知:OE是△ABC的中位线,
∴OE=![]() AB,
AB,
∵AB=![]() BC,
BC,
∴OE=![]() BC=
BC=![]() AD,
AD,
故④正确;
正确的有:①②③④,
故选D.


科目:初中数学 来源: 题型:
【题目】数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为a、宽为b的长方形.用A种纸片- -张,B种纸片一张,C种纸片两张可拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积(答案直接填写到题中横线上);
方法1_________________;
方法2______________________.
(2)观察图2,请你直接写出下列三个代数式: (a+b)2, a2+b2, ab之间的等量关系;
(3)类似的,请你用图1中的三种纸片拼一个图形验证: (a+b)(a+2b)=a2 + 3ab+2b2,请你将该示意图画在答题卡上;
(4)根据(2)题中的等量关系,解决如下问题:
①已知: a+b=5,a2+b2=11, 求ab的值:
②已知(x- 2018)2 +(x- 2020)2=34,求(x- 2019)2的值,

查看答案和解析>>
科目:初中数学 来源: 题型:
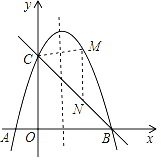
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,已知A(﹣1,0),C(0,3)
(1)求该抛物线的表达式;
(2)求BC的解析式;
(3)点M是对称轴右侧点B左侧的抛物线上一个动点,当点M运动到什么位置时,△BCM的面积最大?求△BCM面积的最大值及此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=10°,点P在OB上.以点P为圆心,OP为半径画弧,交OA于点P1(点P1与点O不重合),连接PP1;再以点P1为圆心,OP为半径画弧,交OB于点P2(点P2与点P不重合),连接P1 P2;再以点P2为圆心,OP为半径画弧,交OA于点P3(点P3与点P1不重合),连接P2 P3;……

请按照上面的要求继续操作并探究:
∠P3 P2 P4=_____°;按照上面的要求一直画下去,得到点Pn,若之后就不能再画出符合要求点Pn+1了,则n=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市对今年“元旦”期间销售A、B、C三种品牌的绿色鸡蛋情况进行了统计,并绘制如图所示的扇形统计图和条形统计图.根据图中信息解答下列问题:
(1)该超市“元旦”期间共销售 个绿色鸡蛋,A品牌绿色鸡蛋在扇形统计图中所对应的扇形圆心角是 度;
(2)补全条形统计图;
(3)如果该超市的另一分店在“元旦”期间共销售这三种品牌的绿色鸡蛋1500个,请你估计这个分店销售的B种品牌的绿色鸡蛋的个数?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)沿海开发公司准备投资开发A、B两种新产品,通过市场调研发现:
(1)若单独投资A种产品,则所获利润yA(万元)与投资金额x(万元)之间满足正比例函数关系:yA=kx;
(2)若单独投资B种产品,则所获利润yB(万元)与投资金额x(万元)之间满足二次函数关系:yB=ax2+bx.
(3)根据公司信息部的报告,yA,yB(万元)与投资金额x(万元)的部分对应值如下表所示:

(1)填空:yA= ;yB= ;
(2)若公司准备投资20万元同时开发A、B两种新产品,设公司所获得的总利润为W(万元),试写出W与某种产品的投资金额x(万元)之间的函数关系式;
(3)请你设计一个在(2)中能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是等边△ABC边AB上的一点,且AD:DB=1:2,现将△ABC折叠,使点C与D重合,折痕为EF,点E、F分别在AC和BC上,则CE:CF的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一棵树高h(m)与生长时间n(年)之间有一定关系,请你根据下表中数据,写出h(m)与n(年)之间的关系式:_____.
n/年 | 2 | 4 | 6 | 8 | … |
h/m | 2.6 | 3.2 | 3.8 | 4.4 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AB两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中l1,l,2表示两人离A地的距离s(m)与时间t(h)的关系,请结合图象解答下列问题:
(1)表示甲离A地的距离与时间关系的图象是 (填l1或l2);甲的速度是 (km/h);乙的速度是 (km/h);
(2)甲出发多长时间后两人相遇?(利用方程解决)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com