
分析 首先根据二次根式有意义的条件可得:$\left\{\begin{array}{l}{x-4≥0}\\{4-x≥0}\end{array}\right.$,解不等式组可得x=4,然后再代入y=$\sqrt{x-4}+\sqrt{4-x}$+1可得y的值,进而可得$\sqrt{x}$+3y的值.
解答 解:由题意得:$\left\{\begin{array}{l}{x-4≥0}\\{4-x≥0}\end{array}\right.$,
解得:x=4,
则y=1,
$\sqrt{x}$+3y=2+3=5.
点评 此题主要考查了二次根式有意义的条件,关键是掌握二次根式中的被开方数是非负数.


科目:初中数学 来源: 题型:选择题
| A. | -π<-3.14<-$\sqrt{3}$ | B. | -3.14<-π<-$\sqrt{3}$ | C. | -3.14<-$\sqrt{3}$<-π | D. | -$\sqrt{3}$<-π<-3.14 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
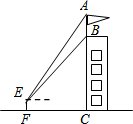 某公司研发一款新型的测角仪,这种测角仪能更精确的测量角度,减少误差.
某公司研发一款新型的测角仪,这种测角仪能更精确的测量角度,减少误差.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com