
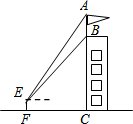
 某公司研发一款新型的测角仪,这种测角仪能更精确的测量角度,减少误差.
某公司研发一款新型的测角仪,这种测角仪能更精确的测量角度,减少误差.分析 (1)过E点作EH⊥BC于H点,在RT△BEH中利用三角函数求得BH的长,然后在直角△EAH中,利用三角函数求得AH的长,根据AB=AH-BH即可求解;
(2)根据机器的总生产量等于机器数与每台生产的产品数即可列方程求解.
解答 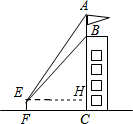 解:(1)过E点作EH⊥BC于H点,
解:(1)过E点作EH⊥BC于H点,
由题:∠AEH=52°,∠BEH=45°,EH=12m,
在RT△BEH中,∵∠BEH=45°
∴BH=EH=12m
在Rt△EAH中,AH=EH•tan52°=15.36m
∴AB=AH-BH≈3.4m
(2)由题意得:40000(1+10%)=400(1-1.25a%)•100(1+2.4a%),
解得:a1=25,a2=$\frac{40}{3}$.
∵20<a<30,
∴a=25.
答:a的值为25.
点评 本题考查了解直角三角形的应用和一元二次方程的应用,正确理解:机器的总生产量等于机器数与每台生产的产品数是关键.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
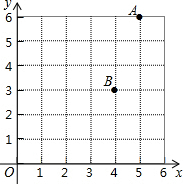 如图是某市两个小区的大致位置示意图,图中点A表示的是茗茗家所居住的小区,点B表示的是茗茗奶奶家所居住的小区,按照先列后行的顺序,点A和点B所在的位置可以表示为( )
如图是某市两个小区的大致位置示意图,图中点A表示的是茗茗家所居住的小区,点B表示的是茗茗奶奶家所居住的小区,按照先列后行的顺序,点A和点B所在的位置可以表示为( )| A. | (6,5)和(3,4) | B. | (5,6)和(3,4) | C. | (6,5)和(4,3) | D. | (5,6)和(4,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com