
【题目】如图,△ABC中,AB=AC=10厘米,BC=12厘米,D是BC的中点,点P从B出发,以a厘米/秒(a>0)的速度沿BA匀速向点A运动,点Q同时以1厘米/秒的速度从D出发,沿DB匀速向点B运动,其中一个动点到达终点时,另一个动点也随之停止运动,设它们的运动时间为t秒.
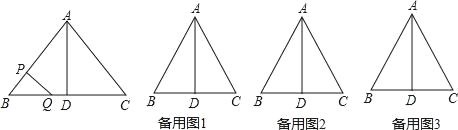
(1)若a=2,那么t为何值时△BPQ与△BDA相似?
(2)已知M为AC上一点,若当t=![]() 时,四边形PQCM是平行四边形,求这时点P的运动速度.
时,四边形PQCM是平行四边形,求这时点P的运动速度.
(3)在P、Q两点运动过程中,要使线段PQ在某一时刻平分△ABD的面积,点P的运动速度应限制在什么范围内?(提示:对于一元二次方程,有如下的结论:若x1x2是方程ax2+bx+c=0(a≠0)的两个根,则x1+x2=﹣![]() ,x1x2=
,x1x2=![]() )
)
【答案】(1)当a=2时,t=![]() 秒或
秒或![]() 秒时,△BPQ与△BDA相似;(2)点P的速度是2.5厘米/秒;(3)点P的速度应大于或等于
秒时,△BPQ与△BDA相似;(2)点P的速度是2.5厘米/秒;(3)点P的速度应大于或等于![]() 厘米/秒.
厘米/秒.
【解析】
(1)根据相似的性质,分情况讨论当△BPQ∽△BDA时及当△BQP∽△BDA时,进行列式计算即可得解;
(2)根据△BPQ∽△BAC,由相似比即可求出P的速度;
(3)根据△BEP∽△BDA,进而求出![]() 和
和![]() 的面积表达式后即可得解.
的面积表达式后即可得解.
(1)当a=2时,BP=2t,DQ=1×t=t,
∵D是BC中点,BC=12,
∴BD=DC=6,
∴![]() ;
;
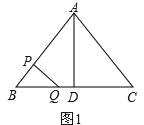
①当△BPQ∽△BDA时,如图1,
则有![]() ,
,
∵BP=2t,BD=6,![]() ,BA=10,
,BA=10,
∴![]() ,
,
解得:![]() ;
;
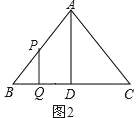
②当△BQP∽△BDA时,如图2,
则有![]() ,
,
∵BP=2t,BD=6,![]() ,BA=10,
,BA=10,
∴![]() ,
,
解得:![]() ;
;
∴当a=2时,![]() 秒或
秒或![]() 秒时,△BPQ与△BDA相似;
秒时,△BPQ与△BDA相似;
(2)当t=![]() 且四边形PQCM是平行四边形时,如图3,
且四边形PQCM是平行四边形时,如图3,
则有PQ∥AC,BP=![]() a,DQ=1×
a,DQ=1×![]() =
=![]() ,BQ=
,BQ=![]() ,
,
∵PQ∥AC,
∴△BPQ∽△BAC,
∴![]() ,
,
∵BP=![]() a,BA=10,BQ=
a,BA=10,BQ=![]() ,BC=12,
,BC=12,
∴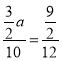 ,
,
解得:a=2.5,
∴点P的速度是2.5厘米/秒;
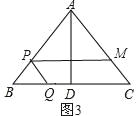
(3)作PE⊥BC,垂足为E,如图4,
∵AB=AC,点D是BC的中点,
∴AD⊥BC,
∵AB=10,BD=6,
∴AD=8,
∵PE⊥BC,AD⊥BC,
∴△BEP∽△BDA,
∴![]() ,
,
∵AD=8,BP=at,BA=10,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵线段PQ平分△ABD的面积,
∴![]() ,
,
∴![]() ,
,
整理得:![]() ,
,
由题可得:![]() ,
,
解得:![]() ,
,
此时![]() ,
,
∴方程![]() 有两个小于6的正实根,
有两个小于6的正实根,
∴点P的速度应大于或等于![]() 厘米/秒.
厘米/秒.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】今年我县为了创建省级文明县城,全面推行中小学校“社会主义核心价值观”进课堂.某校对全校学生进行了检测评价,检测结果分为![]() (优秀)、
(优秀)、![]() (良好)、
(良好)、![]() (合格)、
(合格)、![]() (不合格)四个等级.并随机抽取若干名学生的检测结果作为样本进行数据处理,制作了如下所示不完整的统计表和统计图.
(不合格)四个等级.并随机抽取若干名学生的检测结果作为样本进行数据处理,制作了如下所示不完整的统计表和统计图.
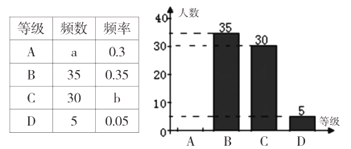
请根据统计表和统计图提供的信息,解答下列问题:
(1)本次随机抽取的样本容量为__________;
(2)统计表中![]() _________,
_________,![]() _________.
_________.
(3)若该校共有学生5000人,请你估算该校学生在本次检测中达到“![]() (优秀)”等级的学生人数.
(优秀)”等级的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解七年级学生的体重情况,随机抽取了七年级m名学生进行调查,将抽取学生的体重情况绘制如下不完整的频数分布表和扇形统计图.
组别 | 体重(千克) | 人数 |
A | 37.5≤x<42.5 | 10 |
B | 42.5≤x<47.5 | n |
C | 47.5≤x<52.5 | 40 |
D | 52.5≤x<57.5 | 20 |
E | 57.5≤x<62.5 | 10 |

请根据图表信息回答下列问题:
(1)填空:①m=_____,②n=_____,③在扇形统计图中,C组所在扇形的圆心角的度数等于_______度;
(2)若把每组中各个体重值用这组数据的中间值代替(例如:A组数据中间值为40千克),则被调查学生的平均体重是多少千克?
(3)如果该校七年级有1000名学生,请估算七年级体重低于47.5千克的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面内容,并解答问题:
杨辉和他的一个数学问题

我国古代对代数的研究,特别是对方程的解法研究有着优良的传统并取得了重要成果.
杨辉,字谦光,钱塘(今浙江杭州)人,南宋杰出的数学家和数学教育家,杨辉一生留下了大量的著述,他著名的数学书共五种二十一卷,它们是:《详解九章算法》12卷(1261年),《日用算法》2卷(1262年),《乘除通变本末》3卷(1274年,第3卷与他人合编),《田(杨辉,南宋数学家)亩比类乘除捷法》2卷(1275年),《续古摘奇算法》2卷(1275年,与他人合编),其中后三种为杨辉后期所著,一般称之为《杨辉算法》.下面是杨辉在1275年提出的一个问题(选自杨辉所著《田亩比类乘除捷法》):
直田积(矩形面积)八百六十四步(平方步),只云阔(宽)不及长一十二步(宽比长少一十二步),问阔及长各几步.
请你用学过的知识解决这个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形;④S四边形ABCD= ![]() AM2.
AM2.
其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
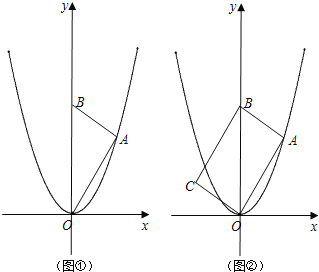
【题目】如图①,在平面直角坐标系中,点A是抛物线y=x2在第一象限上的一个点,连结OA,过点A作AB⊥OA,交y轴于点B,设点A的横坐标为n.
(探究):
(1)当n=1时,点B的纵坐标是 ;
(2)当n=2时,点B的纵坐标是 ;
(3)点B的纵坐标是 (用含n的代数式表示).
(应用):
如图②,将△OAB绕着斜边OB的中点顺时针旋转180°,得到△BCO.
(1)求点C的坐标(用含n的代数式表示);
(2)当点A在抛物线上运动时,点C也随之运动.当1≤n≤5时,线段OC扫过的图形的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“双十一”购物街中,某儿童品牌玩具专卖店购进了![]() 两种玩具,其中
两种玩具,其中![]() 类玩具的金价比
类玩具的金价比![]() 玩具的进价每个多
玩具的进价每个多![]() 元.经调查发现:用
元.经调查发现:用![]() 元购进
元购进![]() 类玩具的数量与用
类玩具的数量与用![]() 元购进
元购进![]() 类玩具的数量相同.
类玩具的数量相同.
(1)求![]() 的进价分别是每个多少元?
的进价分别是每个多少元?
(2)该玩具店共购进![]() 了两类玩具共
了两类玩具共![]() 个,若玩具店将每个
个,若玩具店将每个![]() 类玩具定价为
类玩具定价为![]() 元出售,每个
元出售,每个![]() 类玩具定价
类玩具定价![]() 元出售,且全部售出后所获得的利润不少于
元出售,且全部售出后所获得的利润不少于![]() 元,则该淘宝专卖店至少购进
元,则该淘宝专卖店至少购进![]() 类玩具多少个?
类玩具多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com