
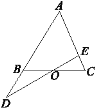
【题目】如图,已知O是△ABC中BC边的中点,且![]() ,则
,则![]() =________.
=________.
【答案】![]()
【解析】过B作BF平行于AC,交DE于点F,由两直线平行内错角相等得到两对内错角相等,再由O为BC的中点,得到BO=CO,利用AAS可得出三角形BOF与三角形COE全等,根据全等三角形对应边相等可得出BF=EC,再由BF平行于AE,得到△DBF∽△DAE,利用相似三角形的性质列出比例式,根据已知AB与AD的比值求出BD与AD的比值,即可得到BF与AE的比值,将BF等量代换为EC,可得出EC与AE的比值,根据比例的性质即可求出AE与AC的比值.
过B作BF∥AC,交DE于点F,
∵BF∥AC,∴∠FBO=∠C,∠BFO=∠CEO,
又O为BC的中点,∴BO=CO,
在△OBF和△OCE中,
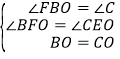 ,∴△OBF≌△OCE(AAS),∴BF=CE,
,∴△OBF≌△OCE(AAS),∴BF=CE,
∵![]() =
=![]() ,∴
,∴![]() =
=![]() ,
,
又∵BF∥AE,∴△DBF∽△DAE,∴![]() =
=![]() =
=![]() =
=![]() ,
,
则![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】阅读理解并解决问题:一般地,如果把一个图形绕着一个定点旋转一定角度![]() (
(![]() 小于
小于![]() )后,能够与原来的图形重合,那么这个图形叫做旋转对称图形,这个定点叫做旋转对称中心.
)后,能够与原来的图形重合,那么这个图形叫做旋转对称图形,这个定点叫做旋转对称中心.![]() 叫做这个旋转对称图形的一个旋转角.请依据上述定义解答下列问题:
叫做这个旋转对称图形的一个旋转角.请依据上述定义解答下列问题:
(1)请写出一个旋转对称图形,这个图形有一个旋转角是![]() .这个图形可以是______;
.这个图形可以是______;
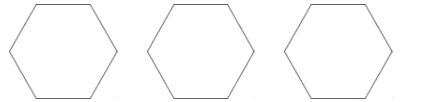
(2)为了美化环境,某中学需要在一块正六边形空地上分别种植六种不同的花草,现将这块空地按下列要求分成六块:①分割后的整个图形必须既是轴对称图形又是旋转对称图形;②六块图形的面积相同.请你按上述两个要求,分别在图中的三个正六边形中画出三种不同的分割方法(只要求画图正确,不写作法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】罚球是篮球比赛中得分的一个组成部分,罚球命中率的高低对篮球比赛的结果影响很大.如图是对某球员罚球训练时命中情况的统计:
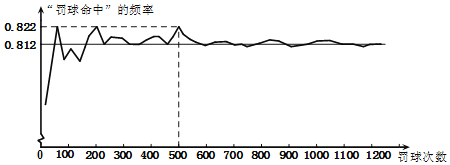
下面三个推断:①当罚球次数是500时,该球员命中次数是411,所以“罚球命中”的概率是0.822;②随着罚球次数的增加,“罚球命中”的频率总在0.812附近摆动,显示出一定的稳定性,可以估计该球员“罚球命中”的概率是0.812;③由于该球员“罚球命中”的频率的平均值是0.809,所以“罚球命中”的概率是0.809.其中合理的是( )
A.①B.②C.①③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
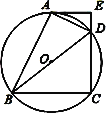
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD交CD的延长线于点E,DA平分∠BDE.
⑴求证:AE是⊙O的切线;
⑵若AE=4cm,CD=6cm,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
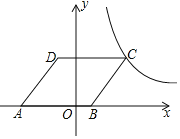
【题目】如图,在平面直角坐标系中,点O为坐标原点,菱形ABCD的顶点B在x轴的正半轴上,点A坐标为(-4,0),点D的坐标为(-1,4),反比例函数![]() 的图象恰好经过点C,则k的值为______.
的图象恰好经过点C,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一张矩形纸片,长10cm,宽6cm,在它的四角各减去一个同样的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面(图中阴影部分)面积是32cm2,求剪去的小正方形的边长.设剪去的小正方形边长是xcm,根据题意可列方程为( )
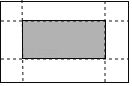
A. 10×6﹣4×6x=32 B. (10﹣2x)(6﹣2x)=32
C. (10﹣x)(6﹣x)=32 D. 10×6﹣4x2=32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b的图象与x轴、y轴分别交于A,B两点,与反比例函数y=![]() 的图象分别交于C,D两点,点C(2,4),点B是线段AC的中点.
的图象分别交于C,D两点,点C(2,4),点B是线段AC的中点.
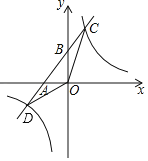
(1)求一次函数y=k1x+b与反比例函数y=![]() 的解析式;
的解析式;
(2)求△COD的面积;
(3)直接写出当x取什么值时,k1x+b<![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为( )
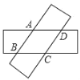
A.5 cmB.4.8 cmC.4.6 cmD.4 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
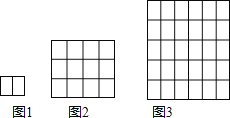
【题目】这样铺地板:第一块铺2块,如图1,第二次把第一次的完全围起来,如图2;第三次把第二次的完全围起来,如图3;…依次方法,铺第5次时需用_____木块才能把第四次所铺的完全围起来.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com