
【题目】今年我县为了创建省级文明县城,全面推行中小学校“社会主义核心价值观”进课堂.某校对全校学生进行了检测评价,检测结果分为![]() (优秀)、
(优秀)、![]() (良好)、
(良好)、![]() (合格)、
(合格)、![]() (不合格)四个等级.并随机抽取若干名学生的检测结果作为样本进行数据处理,制作了如下所示不完整的统计表和统计图.
(不合格)四个等级.并随机抽取若干名学生的检测结果作为样本进行数据处理,制作了如下所示不完整的统计表和统计图.
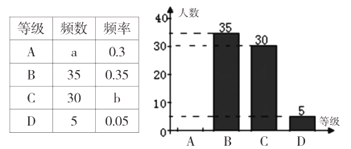
请根据统计表和统计图提供的信息,解答下列问题:
(1)本次随机抽取的样本容量为__________;
(2)统计表中![]() _________,
_________,![]() _________.
_________.
(3)若该校共有学生5000人,请你估算该校学生在本次检测中达到“![]() (优秀)”等级的学生人数.
(优秀)”等级的学生人数.
科目:初中数学 来源: 题型:
【题目】小明同学以“你最喜欢的运动项目”为主题,对公园里参加运动的群众进行随机调查(每名被调查者只能选一个项目,且被调查者都进行了选择).下面是小明根据调查结果列出的统计表和绘制的扇形统计图(不完整).
被调查者男、女所选项目人数统计表
项目 | 男(人数) | 女(人数) |
广场舞 | 7 | 9 |
健步走 |
| 4 |
器械 | 2 | 2 |
跑步 | 5 |
|

根据以上信息回答下列问题:
(1)统计表中的![]() __________,
__________,![]() __________.
__________.
(2)扇形统计图中“广场舞”项目所对应扇形的圆心角度数为__________°.
(3)若平均每天来该公园运动的人数有3600人,请你估计这3600人中最喜欢的运动项目是“跑步”的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
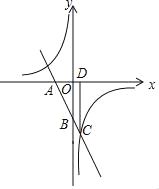
【题目】如图,在平面直角坐标系xOy中,直线AB与x轴、y轴分别交于点A、B,与反比例函数y=![]() 的图象在第四象限交于点C,CD⊥x轴于点D,tan∠OAB=2,OA=2,OD=1.
的图象在第四象限交于点C,CD⊥x轴于点D,tan∠OAB=2,OA=2,OD=1.
(1)求该反比例函数的表达式;
(2)点M是这个反比例函数图象上的点,过点M作MN⊥y轴,垂足为点N,连接OM、AN,如果S△ABN=2S△OMN,直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠DAB=60°,AB=8,AD=6.⊙O分别切边AB,AD于点E,F,且圆心O好落在DE上.现将⊙O沿AB方向滚动到与BC边相切(点O在ABCD的内部),则圆心O移动的路径长为( )

A.2B.4C.5﹣![]() D.8﹣2
D.8﹣2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB是直径,C为![]() 的中点,延长AD,BC交于点P,连结AC.
的中点,延长AD,BC交于点P,连结AC.
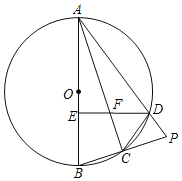
(1)求证:AB=AP;
(2)若AB=10,DP=2,
①求线段CP的长;
②过点D作DE⊥AB于点E,交AC于点F,求△ADF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中
中![]() .点
.点![]() 从点
从点![]() 出发以
出发以![]() 的速度向点
的速度向点![]() 运动,以
运动,以![]() 为一边在
为一边在![]() 的右下方作正方形
的右下方作正方形![]() .同时垂直于
.同时垂直于![]() 的直线
的直线![]() 从点
从点![]() 出发以
出发以![]() 的速度向点
的速度向点![]() 运动,当直线
运动,当直线![]() 和正方形
和正方形![]() 开始有公共点时,点
开始有公共点时,点![]() 运动的时间为__________
运动的时间为__________![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接2022年冬奥会,鼓励更多的学生参与到志愿服务中来,甲、乙两所学校组织了志愿服务团队选拔活动.为了了解两所学校学生的整体情况,从两校进入综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
a.甲学校学生成绩的频数分布直方图如图:

b.甲学校学生成绩在80~90这一组的是:
80 | 80 | 81 | 81 | 82 | 82 | 83 | 83 |
85 | 86 | 86 | 87 | 88 | 88 | 89 | 89 |
c.乙学校学生成绩的平均数、中位数、众数、优秀率(85分及以上为优秀)如下:
平均数 | 中位数 | 众数 | 优秀率 |
85 | 84 | 78 | 46% |
根据以上信息,回答下列问题:
(1)甲学校学生成绩的中位数为 分;
(2)甲学校学生A、乙学校学生B的综合素质展示成绩同为83分,这两人在本校学生中的综合素质展示排名更靠前的是 (填“A”或“B”);
(3)根据上述信息,推断哪所学校综合素质展示的水平更高,并至少从两个不同的角度说明推断的合理性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
(1)若点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,则线段
的中点,则线段![]() 与
与![]() 的数量关系是 ;线段
的数量关系是 ;线段![]() 与
与![]() 的位置关系是 ;
的位置关系是 ;
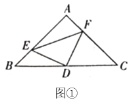
(2)如图①,若点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,且
上的点,且![]() ,上述结论是否依然成立,若成立,请证明;若不成立,请说明理由;
,上述结论是否依然成立,若成立,请证明;若不成立,请说明理由;
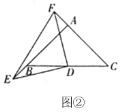
(3)如图②,若点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 延长线上的点,且
延长线上的点,且![]() ,直接写出
,直接写出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=10厘米,BC=12厘米,D是BC的中点,点P从B出发,以a厘米/秒(a>0)的速度沿BA匀速向点A运动,点Q同时以1厘米/秒的速度从D出发,沿DB匀速向点B运动,其中一个动点到达终点时,另一个动点也随之停止运动,设它们的运动时间为t秒.
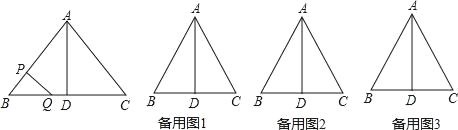
(1)若a=2,那么t为何值时△BPQ与△BDA相似?
(2)已知M为AC上一点,若当t=![]() 时,四边形PQCM是平行四边形,求这时点P的运动速度.
时,四边形PQCM是平行四边形,求这时点P的运动速度.
(3)在P、Q两点运动过程中,要使线段PQ在某一时刻平分△ABD的面积,点P的运动速度应限制在什么范围内?(提示:对于一元二次方程,有如下的结论:若x1x2是方程ax2+bx+c=0(a≠0)的两个根,则x1+x2=﹣![]() ,x1x2=
,x1x2=![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com