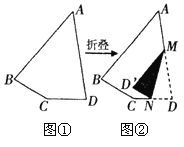
【题目】如图①，一张四边形纸片ABCD，∠A＝50°，∠C＝150°．若将其按照图②所示方式折叠后，恰好MD′∥AB，ND′∥BC，则∠D的度数为 ．
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案科目：初中数学 来源： 题型：
【题目】阅读材料：善于思考的小军在解方程组
时，采用了一种“整体代换”的解法：
解：将方程②变形为4x＋10y＋y＝5，即2(2x＋5y)＋y＝5， ③
把方程①代入③得2×3＋y＝5，∴y＝－1，
把y＝－1代入①得x＝4，
∴方程组的解为
请你解决以下问题：
(1)模仿小军的“整体代换”法解方程组
(2)已知x，y满足方程组
求整式x2＋4y2＋xy的值；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类)，发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式． 比如图②可以解释为：（a+2b）（a+b）=a2+3ab+2b2
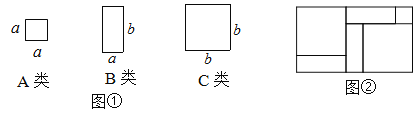
(1)取图①中的若干个(三种图形都要取到)拼成一个长方形，使它的边长分别为(2a+b)、(a+2b)，不画图形，试通过计算说明需要C类卡片多少张；
(2)若取其中的若干个(三种图形都要取到)拼成一个长方形，使它的面积等于a2＋5ab＋4b2，画出这个长方形，并根据图形对多项式a2＋5ab＋4b2进行因式分解；
(3) 如图③，大正方形的边长为m，小正方形的边长为n，若用x、y表示四个矩形的两边长（x>y），观察图案并判断，将正确关系式的序号填写在横线上______ _____（填写序号）
①．xy =
②．x+y=m ③．x2－y2=m·n ④．x2+y2 =
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在矩形AOBC中，OB=6，OA=4，分别以OB，OA所在直线为x轴和y轴，建立如图所示的平面直角坐标系．F是边BC上一点（不与B、C两点重合），过点F的反比例函数y=
（k＞0）图象与AC边交于点E．
（1）请用k的表示点E，F的坐标；
（2）若△OEF的面积为9，求反比例函数的解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把几个图形拼成一个新的图形，再通过两种不同的方法计算同一个图形的面积，可以得到一个等式，也可以求出一些不规则图形的面积．
例如，由图1，可得等式：（a+2b）（a+b）=a2+3ab+2b2
（1）如图2，将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形，试用不同的形式表示这个大正方形的面积，你能发现什么结论？请用等式表示出来．
（2）利用（1）中所得到的结论，解决下面的问题： 已知a+b+c=11，ab+bc+ac=38，求a2+b2+c2的值．
（3）如图3，将两个边长分别为a和b的正方形拼在一起，B，C，G三点在同一直线上，连接BD和BF．若这两个正方形的边长满足a+b=10，ab=20，请求出阴影部分的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
