
【题目】在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() (
(![]() )的一个交点为
)的一个交点为![]() .
.
(1)求k的值;
(2)将直线![]() 向上平移b(b>0)个单位长度后,与x轴,y轴分别交于点A,点B,与双曲线
向上平移b(b>0)个单位长度后,与x轴,y轴分别交于点A,点B,与双曲线![]() (
(![]() )的一个交点记为Q.若
)的一个交点记为Q.若![]() ,求b的值.
,求b的值.
科目:初中数学 来源: 题型:
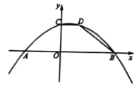
【题目】如图抛物线![]() 的开口向下与
的开口向下与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线上一个动点(不与点
是抛物线上一个动点(不与点![]() 重合)
重合)

(1)求抛物线的解析式;
(2)当点![]() 是抛物线上一个动点,若
是抛物线上一个动点,若![]() 的面积为12,求点
的面积为12,求点![]() 的坐标;
的坐标;
(3)如图2,抛物线的顶点为![]() ,在抛物线上是否存在点
,在抛物线上是否存在点![]() ,使得
,使得![]() ,若存在请直接写出点
,若存在请直接写出点![]() 的坐标;若不存在请说明理由.
的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是
是![]() 所对弦
所对弦![]() 上一动点,点
上一动点,点![]() 在
在![]() 的延长线上,过点
的延长线上,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,已知
,已知![]() ,
,![]() ,设
,设![]() ,
,![]() 两点间的距离为
两点间的距离为![]() ,
,![]() 的面积为
的面积为![]() .(当点
.(当点![]() 与点
与点![]() ,
,![]() 重合时,
重合时,![]() 的值为0.)
的值为0.)

小亮根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小亮的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 4.47 | 7.07 | 9.00 | 8.94 | 0 |
(2)在平面直角坐标系中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当![]() 的面积为
的面积为![]() 时,
时,![]() 的长度约为
的长度约为 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,老师提出问题:如图1,在Rt△ABC中,∠C=90°,BC=4cm,AC=3cm,点D是AB的中点,点E是BC上一个动点,连接AE、DE.问CE的长是多少时,△AED的周长等于CE长的3倍.设CE=xcm,△AED的周长为ycm(当点E与点B重合时,y的值为10).
小牧根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小牧的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
y/cm | 8.0 | 7.7 | 7.5 | 7.4 |
| 8.0 | 8.6 | 9.2 | 10 |
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出上表中对应值为坐标的点,画出该函数的图象,如图2;
(3)结合画出的函数图象,解决问题:
①当CE的长约为 cm时,△AED的周长最小;
②当CE的长约为 cm时,△AED的周长等于CE的长的3倍.
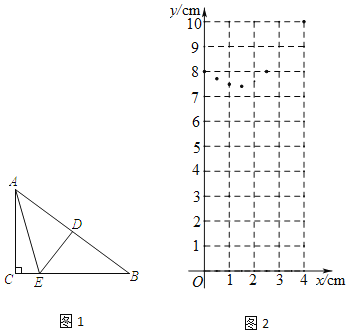
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若存在过点P的直线l交⊙C于异于点P的A,B两点,在P,A,B三点中,位于中间的点恰为以另外两点为端点的线段的中点时,则称点P为⊙C 的相邻点,直线l为⊙C关于点P的相邻线.
(1)当⊙O的半径为1时,
①分别判断在点D(![]() ,
,![]() ),E(0,
),E(0,![]() ),F(4,0)中,是⊙O的相邻点有__________;
),F(4,0)中,是⊙O的相邻点有__________;
②请从①中的答案中,任选一个相邻点,在图1中做出⊙O关于它的一条相邻线,并说明你的作图过程.
③点P在直线![]() 上,若点P为⊙O的相邻点,求点P横坐标的取值范围;
上,若点P为⊙O的相邻点,求点P横坐标的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线![]() 与x轴,y轴分别交于点M,N,若线段MN上存在⊙C的相邻点P,直接写出圆心C的横坐标的取值范围.
与x轴,y轴分别交于点M,N,若线段MN上存在⊙C的相邻点P,直接写出圆心C的横坐标的取值范围.
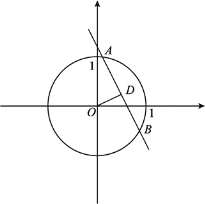
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在浙江卫视全新推出的大型户外竞技真人秀节目﹣﹣《奔跑吧兄弟》中,七位主持人邓超、王祖蓝、王宝强、李晨、陈赫、郑凯及Angelababy(杨颖)在“撕名牌环节”的成绩分别为:8,5,7,8,6,8,5,则这组数据的众数和中位数分别是 .
(2)某学校想了解学生对撕名牌游戏的喜欢程度,对学校部分学生进行了抽样调查,就学生对游戏的喜欢程度(A:喜欢;B:一般;C:不喜欢;D:无所谓)进行数据统计,并绘制了如下两幅不完整的统计图.
①此次调查的样本容量为 ;
②条形统计图中存在的错误是 (填A、B、C中的一个);
③在图2中补画条形统计图中不完整的部分;
④若从该校喜欢撕名牌游戏的学生中抽取10人进行比赛,则喜欢撕名牌游戏的小明被抽中的概率是多少?
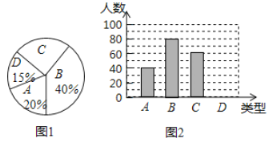
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() 、
、![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,过点
,过点![]() 作
作![]() ,与抛物线相交于点
,与抛物线相交于点![]() .点
.点![]() 从点
从点![]() 出发,在折线段
出发,在折线段![]() 上以每秒2个单位长度向終点
上以每秒2个单位长度向終点![]() 勾速运动,点
勾速运动,点![]() 从点
从点![]() 出发,在线段
出发,在线段![]() 上以每秒1个单位长度向终点
上以每秒1个单位长度向终点![]() 匀速运动,两点同时出发,当其中一个点到达终点时,另一个点也停止运动,连接
匀速运动,两点同时出发,当其中一个点到达终点时,另一个点也停止运动,连接![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() ,线段
,线段![]() 的长度的平方为
的长度的平方为![]() ,即
,即![]() (单位长度
(单位长度![]() ),
),
(1)求线段![]() 的长;
的长;
(2)求![]() 关于
关于![]() 的函数解析式,并直接写出自变量
的函数解析式,并直接写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两工程队共同承建某高速路隧道工程,隧道总长2000米,甲、乙分别从隧道两端向中间施工,计划每天各施工6米.因地质情况不同,两支队伍每合格完成1米隧道施工所需成本不一样.甲每合格完成1米,隧道施工成本为6万元;乙每合格完成1米,隧道施工成本为8万元.
(1)若工程结算时乙总施工成本不低于甲总施工成本的![]() ,求甲最多施工多少米?
,求甲最多施工多少米?
(2)实际施工开始后因地质情况比预估更复杂,甲乙两队每日完成量和成本都发生变化.甲每合格完成1米隧道施工成本增加m万元时,则每天可多挖![]() m米,乙因特殊地质,在施工成本不变的情况下,比计划每天少挖
m米,乙因特殊地质,在施工成本不变的情况下,比计划每天少挖![]() m米,若最终每天实际总成本比计划多(11m-8)万元,求m的值.
m米,若最终每天实际总成本比计划多(11m-8)万元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】改革开放40年来,中国已经成为领先世界的基建强国,如图①是建筑工地常见的塔吊,其主体部分的平面示意图如图②,点F在线段HG上运动,BC∥HG,AE⊥BC,垂足为点E,AE的延长线交HG于点G,经测量,∠ABD=11°,∠ADE=26°,∠ACE=31°,BC=20m,EG=0.6m.
(1)求线段AG的长度;
(2)连接AF,当线段AF⊥AC时,求点F和点G之间的距离.
(所有结果精确到0.1m.参考数据:tan11°≈0.19,tan26°≈0.49,tan31°≈0.60)
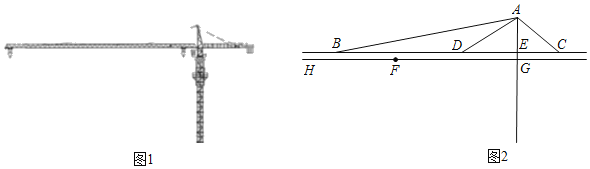
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com