
【题目】甲、乙两工程队共同承建某高速路隧道工程,隧道总长2000米,甲、乙分别从隧道两端向中间施工,计划每天各施工6米.因地质情况不同,两支队伍每合格完成1米隧道施工所需成本不一样.甲每合格完成1米,隧道施工成本为6万元;乙每合格完成1米,隧道施工成本为8万元.
(1)若工程结算时乙总施工成本不低于甲总施工成本的![]() ,求甲最多施工多少米?
,求甲最多施工多少米?
(2)实际施工开始后因地质情况比预估更复杂,甲乙两队每日完成量和成本都发生变化.甲每合格完成1米隧道施工成本增加m万元时,则每天可多挖![]() m米,乙因特殊地质,在施工成本不变的情况下,比计划每天少挖
m米,乙因特殊地质,在施工成本不变的情况下,比计划每天少挖![]() m米,若最终每天实际总成本比计划多(11m-8)万元,求m的值.
m米,若最终每天实际总成本比计划多(11m-8)万元,求m的值.
【答案】(1)1000米;(2)4
【解析】
(1)设甲工程队施工x米,则乙工程队施工(2000-x)米,由工程结算时乙总施工成本不低于甲总施工成本的![]() ,即可得出关于x的一元一次不等式,解之取其中的最大值即可得出结论;
,即可得出关于x的一元一次不等式,解之取其中的最大值即可得出结论;
(2)根据总成本=每米施工成本×每天施工的长度结合每天实际总成本比计划多(11m-8)万元,即可得出关于m的一元二次方程,解之即可得出结论.
解:(1)设甲工程队施工x米,则乙工程队施工(2000-x)米,
依题意,得:8(2000-x)≥![]() ×6x,
×6x,
解得:x≤1000.
答:甲最多施工1000米.
(2)依题意,得:(6+m)(6+![]() m)+8(6-
m)+8(6-![]() m)=6×(6+8)+11m-8,
m)=6×(6+8)+11m-8,
整理,得:m2-8m+16=0,
解得:m1=m2=4.
答:m的值为4.


科目:初中数学 来源: 题型:
【题目】如图,正方形纸片![]() 的边长为
的边长为![]() ,翻折
,翻折![]() ,使两个直角顶点重合于对角线
,使两个直角顶点重合于对角线![]() 上一点
上一点![]() 分别是折痕,设
分别是折痕,设![]() ,给出下列判断:
,给出下列判断:
①当![]() 时,点
时,点![]() 是正方形
是正方形![]() 的中心;
的中心;
②当![]() 时,
时,![]() ;
;
③当![]() 时,六边形
时,六边形![]() 面积的最大值是
面积的最大值是![]()
④当![]() 时,六边形
时,六边形![]() 周长的值不变.
周长的值不变.
其中错误的是( )

A.②③B.③④C.①④D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() (
(![]() )的一个交点为
)的一个交点为![]() .
.
(1)求k的值;
(2)将直线![]() 向上平移b(b>0)个单位长度后,与x轴,y轴分别交于点A,点B,与双曲线
向上平移b(b>0)个单位长度后,与x轴,y轴分别交于点A,点B,与双曲线![]() (
(![]() )的一个交点记为Q.若
)的一个交点记为Q.若![]() ,求b的值.
,求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,Rt△ABC中,∠ACB=90°,AC=5,BC=12,点D在边AB上,以AD为直径的⊙O,与边BC有公共点E,则AD的最小值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
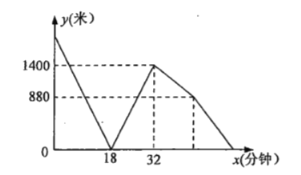
【题目】甲,乙两人分别从![]() ,
,![]() 两地相向而行,甲先走3分钟后乙才开始行走,甲到达
两地相向而行,甲先走3分钟后乙才开始行走,甲到达![]() 地后立即停止,乙到达
地后立即停止,乙到达![]() 地后立即以另一速度返回
地后立即以另一速度返回![]() 地,在整个行驶的过程中,两人保持各自速度匀速行走,甲,乙两人之间的距离
地,在整个行驶的过程中,两人保持各自速度匀速行走,甲,乙两人之间的距离![]() (米)与乙出发的时间
(米)与乙出发的时间![]() (分钟)的函数关系如图所示.当甲到达
(分钟)的函数关系如图所示.当甲到达![]() 地时,则乙距离
地时,则乙距离![]() 地的时间还需要________分钟.
地的时间还需要________分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把三角形按如图所示的规律拼图案,其中第①个图案中有4个三角形,第②个图案中有6个三角形,第③个图案中有8个三角形,…,按此规律排列下去,则第⑦个图案中三角形的个数为( )
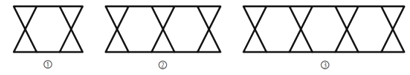
A. 12 B. 14 C. 16 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
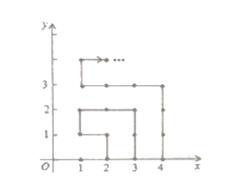
【题目】如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“![]() ”方向排列,如
”方向排列,如![]() ······根据这个规律,第
······根据这个规律,第![]() 个点的纵坐标为( )
个点的纵坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com