
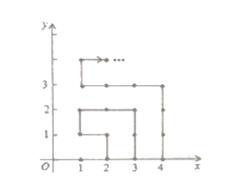
【题目】如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“![]() ”方向排列,如
”方向排列,如![]() ······根据这个规律,第
······根据这个规律,第![]() 个点的纵坐标为( )
个点的纵坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
观察图形可知,以最外边的矩形边长上的点为准,点的总个数等于x轴上右下角的点的横坐标的平方,并且右下角的点的横坐标是奇数时最后以横坐标为该数,纵坐标为0结束,当右下角的点横坐标是偶数时,以横坐标为1,纵坐标为右下角横坐标的偶数减1的点结束,根据此规律解答即可.
解:根据图形,以最外边的矩形边长上的点为准,点的总个数等于x轴上右下角的点的横坐标的平方,
例如:右下角的点的横坐标为1,共有1个,1=12,
右下角的点的横坐标为2时,共有4个,4=22,
右下角的点的横坐标为3时,共有9个,9=32,
右下角的点的横坐标为4时,共有16个,16=42,
…
右下角的点的横坐标为n时,共有n2个,
∵452=2025,45是奇数,
∴第2025个点是(45,0),
第2019个点是(45,6),
所以,第2019个点的纵坐标为6.
故选:B.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两工程队共同承建某高速路隧道工程,隧道总长2000米,甲、乙分别从隧道两端向中间施工,计划每天各施工6米.因地质情况不同,两支队伍每合格完成1米隧道施工所需成本不一样.甲每合格完成1米,隧道施工成本为6万元;乙每合格完成1米,隧道施工成本为8万元.
(1)若工程结算时乙总施工成本不低于甲总施工成本的![]() ,求甲最多施工多少米?
,求甲最多施工多少米?
(2)实际施工开始后因地质情况比预估更复杂,甲乙两队每日完成量和成本都发生变化.甲每合格完成1米隧道施工成本增加m万元时,则每天可多挖![]() m米,乙因特殊地质,在施工成本不变的情况下,比计划每天少挖
m米,乙因特殊地质,在施工成本不变的情况下,比计划每天少挖![]() m米,若最终每天实际总成本比计划多(11m-8)万元,求m的值.
m米,若最终每天实际总成本比计划多(11m-8)万元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】改革开放40年来,中国已经成为领先世界的基建强国,如图①是建筑工地常见的塔吊,其主体部分的平面示意图如图②,点F在线段HG上运动,BC∥HG,AE⊥BC,垂足为点E,AE的延长线交HG于点G,经测量,∠ABD=11°,∠ADE=26°,∠ACE=31°,BC=20m,EG=0.6m.
(1)求线段AG的长度;
(2)连接AF,当线段AF⊥AC时,求点F和点G之间的距离.
(所有结果精确到0.1m.参考数据:tan11°≈0.19,tan26°≈0.49,tan31°≈0.60)
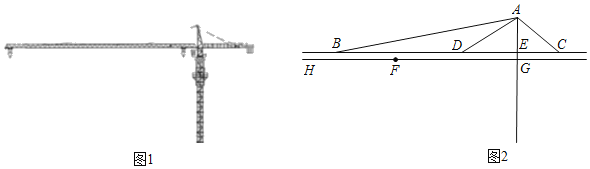
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在某一路段,规定汽车限速行驶,交通警察在此限速路段的道路上设置了监测区,其中点C、D为监测点,已知点C、D、B在同一直线上,且AC⊥BC,CD=400米,tan∠ADC=2,∠ABC=35°
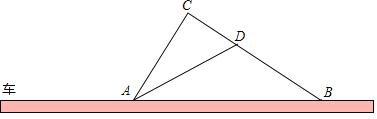
(1)求道路AB段的长(结果精确到1米)
(2)如果道路AB的限速为60千米/时,一辆汽车通过AB段的时间为90秒,请你判断该车是否是超速,并说明理由;参考数据:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
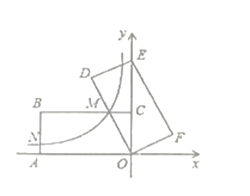
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 分别在
分别在![]() 轴的负半轴、
轴的负半轴、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在第二象限.将矩形
在第二象限.将矩形![]() 绕点
绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 落在
落在![]() 轴上,得到矩形
轴上,得到矩形![]() 与
与![]() 相交于点
相交于点![]() .若经过点
.若经过点![]() 的反比例函数
的反比例函数![]() 的图象交
的图象交![]() 于点
于点![]() 的图象交
的图象交![]() 于点
于点![]()
![]() 则
则![]() 的长为____.
的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在一次数学兴趣小组活动中,对一个数学问题作如下探究:
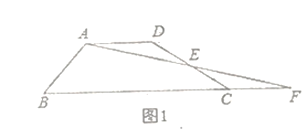
问题情境:(1)如图1,四边形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边的中点,连接
边的中点,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() ,求证:
,求证:![]() ;(
;(![]() 表示面积)
表示面积)
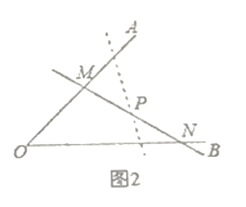
问题迁移:(2)如图2:在已知锐角![]() 内有一个定点
内有一个定点![]() .过点
.过点![]() 任意作一条直线
任意作一条直线![]() 分别交射线
分别交射线![]() 于点
于点![]() .小明将直线
.小明将直线![]() 绕着点
绕着点![]() 旋转的过程中发现,
旋转的过程中发现,![]() 的面积存在最小值,请问当直线
的面积存在最小值,请问当直线![]() 在什么位置时,
在什么位置时,![]() 的面积最小,并说明理由.
的面积最小,并说明理由.
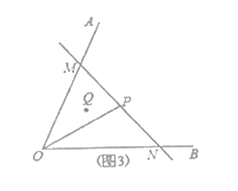
实际应用:(3)如图3,若在道路![]() 之间有一村庄
之间有一村庄![]() 发生疫情,防疫部门计划以公路
发生疫情,防疫部门计划以公路![]() 和经过防疫站
和经过防疫站![]() 的一条直线
的一条直线![]() 为隔离线,建立个面积最小的三角形隔离区
为隔离线,建立个面积最小的三角形隔离区![]() ,若测得
,若测得![]() 试求
试求![]() 的面积.(结果保留根号)(参考数据:
的面积.(结果保留根号)(参考数据:![]() )
)
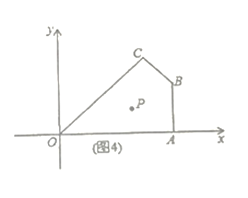
拓展延伸:(4)如图4,在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() 的坐标分别为
的坐标分别为![]() ,过点
,过点![]() 的直线
的直线![]() 与四边形
与四边形![]() 一组对边相交,将四边形
一组对边相交,将四边形![]() 分成两个四边形,求其中以点
分成两个四边形,求其中以点![]() 为顶点的四边形面积的最大值.
为顶点的四边形面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:sin(﹣x)=﹣sinx,cos(﹣x)=cosx,sin(x+y)=sinxcosy+cosxsiny.
据此判断下列等式成立的是 (写出所有正确的序号)
①cos(﹣60°)=﹣![]() ;
;
②sin75°=![]() ;
;
③sin2x=2sinxcosx;
④sin(x﹣y)=sinxcosy﹣cosxsiny.
查看答案和解析>>
科目:初中数学 来源: 题型:
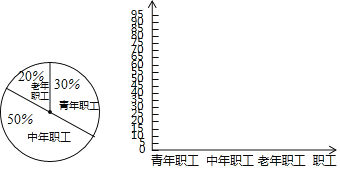
【题目】某单位有职工200人,其中青年职工(20﹣35岁),中年职工(35﹣50岁),老年职工(50岁及 以上)所占比例如扇形统计图所示.
为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小张抽样调查单位3名职工的健康指数
年龄 | 26 | 42 | 57 |
健康指数 | 97 | 79 | 72 |
表2:小王抽样调查单位10名职工的健康指数
年龄 | 23 | 25 | 26 | 32 | 33 | 37 | 39 | 42 | 48 | 52 |
健康指数 | 93 | 89 | 90 | 83 | 79 | 75 | 80 | 69 | 68 | 60 |
表3:小李抽样调查单位10名职工的健康指数
年龄 | 22 | 29 | 31 | 36 | 39 | 40 | 43 | 46 | 51 | 55 |
健康指数 | 94 | 90 | 88 | 85 | 82 | 78 | 72 | 76 | 62 | 60 |
根据上述材料回答问题:
(1)小张、小王和小李三人中,谁的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.
(2)根据能够较好地反映出该单位职工健康情况表,绘制出青年职工、中年职工、老年职工健康指数的平均数的直方图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com