
【题目】已知![]() 在半径为1的
在半径为1的![]() 上,直线
上,直线![]() 与
与![]() 相切,
相切,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
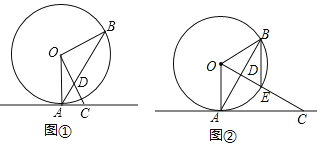
(Ⅰ)如图①,若![]() ,求
,求![]() 的长;
的长;
(Ⅱ)如图②,![]() 与
与![]() 交于点
交于点![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() -1.
-1.
【解析】
(1)由切线的性质可知∠OAC=90°,由三角形的内角和定理可知∠AOC=30°,由∠AOB=∠AOC+∠BOC可得出∠AOB的度数,结合OA=OB可得出∠OAB=∠OBA=30°,由此可得出OD=AD,由∠OAB与∠DAC互余可知∠DAC=60°=∠DCA,由此得出△DAC为等边三角形,从而得出OD=AC,由特殊角的三角函数值即可得出结论;
(2)由OC⊥OB且OC=OB可知∠OBE=∠OEB=45°,再由BE∥OA可得出∠AOC=45°,结合切线性质可得出OA=AC,根据角与角之间的关系逐步得出∠CAD=∠CDA=67.5°,由此可得出AC=CD,结合勾股定理即可得出结论.
解:(1)∵AC与⊙O相切,
∴∠OAC=90°.
∵∠OCA=60°,
∴∠AOC=30°.
∵OC⊥OB,
∴∠AOB=∠AOC+∠BOC=120°.
∵OA=OB,
∴∠OAB=∠OBA=30°,
∴OD=AD,∠DAC=60°
∴AD=CD=AC.
∵OA=1,
∴OD=AC=OAtan∠AOC=![]() .
.
(2)∵OC⊥OB,
∴∠OBE=∠OEB=45°.
∵BE∥OA,
∴∠AOC=45°,∠ABE=∠OAB,
∴OA=AC,∠OAB=∠OBA=22.5°,
∴∠ADC=∠AOC+∠OAB=67.5°.
∵∠DAC=90°-∠OAB=67.5°=∠ADC,
∴AC=CD.
∵OC=![]() =
=![]() ,
,
∴OD=OC-CD=![]() -1.
-1.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,点![]() 是
是![]() 所对弦
所对弦![]() 上一动点,点
上一动点,点![]() 在
在![]() 的延长线上,过点
的延长线上,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,已知
,已知![]() ,
,![]() ,设
,设![]() ,
,![]() 两点间的距离为
两点间的距离为![]() ,
,![]() 的面积为
的面积为![]() .(当点
.(当点![]() 与点
与点![]() ,
,![]() 重合时,
重合时,![]() 的值为0.)
的值为0.)

小亮根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小亮的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 4.47 | 7.07 | 9.00 | 8.94 | 0 |
(2)在平面直角坐标系中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
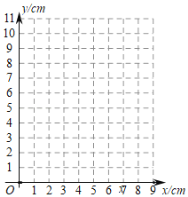
(3)结合画出的函数图象,解决问题:当![]() 的面积为
的面积为![]() 时,
时,![]() 的长度约为
的长度约为 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() 、
、![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,过点
,过点![]() 作
作![]() ,与抛物线相交于点
,与抛物线相交于点![]() .点
.点![]() 从点
从点![]() 出发,在折线段
出发,在折线段![]() 上以每秒2个单位长度向終点
上以每秒2个单位长度向終点![]() 勾速运动,点
勾速运动,点![]() 从点
从点![]() 出发,在线段
出发,在线段![]() 上以每秒1个单位长度向终点
上以每秒1个单位长度向终点![]() 匀速运动,两点同时出发,当其中一个点到达终点时,另一个点也停止运动,连接
匀速运动,两点同时出发,当其中一个点到达终点时,另一个点也停止运动,连接![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() ,线段
,线段![]() 的长度的平方为
的长度的平方为![]() ,即
,即![]() (单位长度
(单位长度![]() ),
),
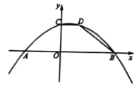
(1)求线段![]() 的长;
的长;
(2)求![]() 关于
关于![]() 的函数解析式,并直接写出自变量
的函数解析式,并直接写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两工程队共同承建某高速路隧道工程,隧道总长2000米,甲、乙分别从隧道两端向中间施工,计划每天各施工6米.因地质情况不同,两支队伍每合格完成1米隧道施工所需成本不一样.甲每合格完成1米,隧道施工成本为6万元;乙每合格完成1米,隧道施工成本为8万元.
(1)若工程结算时乙总施工成本不低于甲总施工成本的![]() ,求甲最多施工多少米?
,求甲最多施工多少米?
(2)实际施工开始后因地质情况比预估更复杂,甲乙两队每日完成量和成本都发生变化.甲每合格完成1米隧道施工成本增加m万元时,则每天可多挖![]() m米,乙因特殊地质,在施工成本不变的情况下,比计划每天少挖
m米,乙因特殊地质,在施工成本不变的情况下,比计划每天少挖![]() m米,若最终每天实际总成本比计划多(11m-8)万元,求m的值.
m米,若最终每天实际总成本比计划多(11m-8)万元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数![]() 的图象,其对称轴为
的图象,其对称轴为![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() 是抛物线上两点,则
是抛物线上两点,则![]() .其中正确的结论有( )
.其中正确的结论有( )
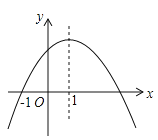
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
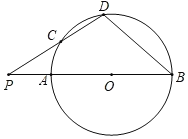
【题目】如图,AB为![]() 的直径,P为BA延长线上的一点,D在
的直径,P为BA延长线上的一点,D在![]() 上(不与点A,点B重合),连结PD交
上(不与点A,点B重合),连结PD交![]() 于点C,且PC=OB.设
于点C,且PC=OB.设![]() ,下列说法正确的是( )
,下列说法正确的是( )
A. 若![]() ,则
,则![]()
B. 若![]() ,则
,则![]()
C. 若![]() ,则
,则![]()
D. 若![]() ,则
,则![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年5月3日,中国科学院在上海发布了中国首款人工智能芯片:寒武纪(MLU100),该芯片在平衡模式下的等效理论峰值速度达每秒128 000 000 000 000次定点运算,将数
128 000 000 000 000用科学计数法表示为( )
A. 1.28![]() 1014 B. 1.28
1014 B. 1.28![]() 10-14 C. 128
10-14 C. 128![]() 1012 D. 0.128
1012 D. 0.128![]() 1011
1011
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】改革开放40年来,中国已经成为领先世界的基建强国,如图①是建筑工地常见的塔吊,其主体部分的平面示意图如图②,点F在线段HG上运动,BC∥HG,AE⊥BC,垂足为点E,AE的延长线交HG于点G,经测量,∠ABD=11°,∠ADE=26°,∠ACE=31°,BC=20m,EG=0.6m.
(1)求线段AG的长度;
(2)连接AF,当线段AF⊥AC时,求点F和点G之间的距离.
(所有结果精确到0.1m.参考数据:tan11°≈0.19,tan26°≈0.49,tan31°≈0.60)
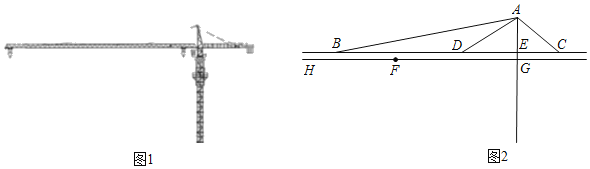
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在一次数学兴趣小组活动中,对一个数学问题作如下探究:
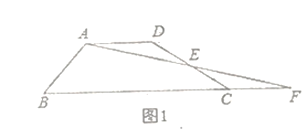
问题情境:(1)如图1,四边形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边的中点,连接
边的中点,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() ,求证:
,求证:![]() ;(
;(![]() 表示面积)
表示面积)
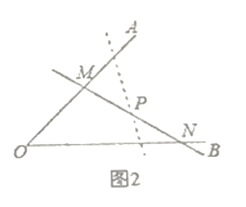
问题迁移:(2)如图2:在已知锐角![]() 内有一个定点
内有一个定点![]() .过点
.过点![]() 任意作一条直线
任意作一条直线![]() 分别交射线
分别交射线![]() 于点
于点![]() .小明将直线
.小明将直线![]() 绕着点
绕着点![]() 旋转的过程中发现,
旋转的过程中发现,![]() 的面积存在最小值,请问当直线
的面积存在最小值,请问当直线![]() 在什么位置时,
在什么位置时,![]() 的面积最小,并说明理由.
的面积最小,并说明理由.
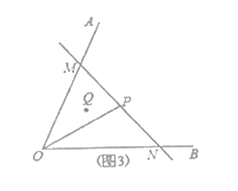
实际应用:(3)如图3,若在道路![]() 之间有一村庄
之间有一村庄![]() 发生疫情,防疫部门计划以公路
发生疫情,防疫部门计划以公路![]() 和经过防疫站
和经过防疫站![]() 的一条直线
的一条直线![]() 为隔离线,建立个面积最小的三角形隔离区
为隔离线,建立个面积最小的三角形隔离区![]() ,若测得
,若测得![]() 试求
试求![]() 的面积.(结果保留根号)(参考数据:
的面积.(结果保留根号)(参考数据:![]() )
)
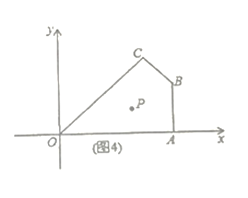
拓展延伸:(4)如图4,在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() 的坐标分别为
的坐标分别为![]() ,过点
,过点![]() 的直线
的直线![]() 与四边形
与四边形![]() 一组对边相交,将四边形
一组对边相交,将四边形![]() 分成两个四边形,求其中以点
分成两个四边形,求其中以点![]() 为顶点的四边形面积的最大值.
为顶点的四边形面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com