
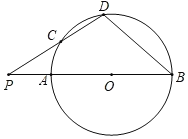
【题目】如图,AB为![]() 的直径,P为BA延长线上的一点,D在
的直径,P为BA延长线上的一点,D在![]() 上(不与点A,点B重合),连结PD交
上(不与点A,点B重合),连结PD交![]() 于点C,且PC=OB.设
于点C,且PC=OB.设![]() ,下列说法正确的是( )
,下列说法正确的是( )
A. 若![]() ,则
,则![]()
B. 若![]() ,则
,则![]()
C. 若![]() ,则
,则![]()
D. 若![]() ,则
,则![]()
【答案】C
【解析】
连接OC,OD.首先证明3α+2β=180°,再一一判断即可.
如图,连接OC,OD.

∵OD=OB,∴∠B=∠ODB=β,∴∠POD=∠B+∠ODB=2β.
∵CP=CO=OD,∴∠P=∠COP=α,∠OCD=∠ODC.
∵∠OCD=∠P+∠COP,∴∠ODC=2α.
∵∠P+∠POD+∠ODP=180°,∴3α+2β=180°①.
不妨设选项A正确,则α=30°,β=30°,显然不满足①,故假设错误.
不妨设B正确,则α=30°,β=60°,显然不满足①,故假设错误.
不妨设C正确,则α=10°,β=75°,满足条件①,故选项C正确.
不妨设B正确,则α=15°,β=45°,显然不满足①,故假设错误.
故选C.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形AOBC中,若∠1=∠2,∠3+∠4=180°,则下列结论正确的有( )
(1)A、O、B、C四点共圆
(2)AC=BC
(3)cos∠1=![]()
(4)S四边形AOBC=![]()
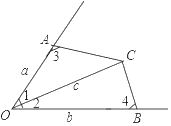
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
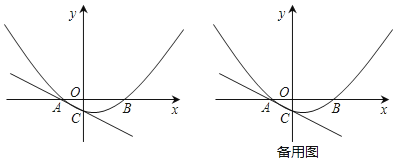
【题目】如图,已知A(﹣2,0),B(4,0),抛物线y=ax2+bx﹣1过A、B两点,并与过A点的直线y=﹣![]() x﹣1交于点C.
x﹣1交于点C.
(1)求抛物线解析式及对称轴;
(2)在抛物线的对称轴上是否存在一点P,使四边形ACPO的周长最小?若存在,求出点P的坐标,若不存在,请说明理由;
(3)点M为y轴右侧抛物线上一点,过点M作直线AC的垂线,垂足为N.问:是否存在这样的点N,使以点M、N、C为顶点的三角形与△AOC相似,若存在,求出点N的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
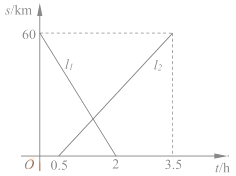
【题目】A、B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中![]() 表示两人离A地的距离S(km)与时间t(h)的关系,结合图像回答下列问题:
表示两人离A地的距离S(km)与时间t(h)的关系,结合图像回答下列问题:
(1)表示乙离开A地的距离与时间关系的图像是________(填![]() );
);
甲的速度是__________km/h;乙的速度是________km/h。
(2)甲出发后多少时间两人恰好相距5km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A重合,两边分别与AB,AC重合.将三角尺绕点A按逆时针方向旋转.
(1)当三角尺的两边分别与菱形的两边BC,CD相交于点E,F时,(如图1),通过观察或测量BE,CF的长度,你能得出什么结论并证明你的结论;
(2)当三角尺的两边分别与菱形的两边BC,CD的延长线相交于点E,F时(如图2),你在(1)中得到的结论还成立吗?简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两条射线BA//CD,PB和PC分别平分∠ABC和∠DCB,AD过点P,分别交AB,CD与点A,D.
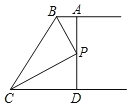
(1)求∠BPC的度数;
(2)若![]() ,求AB+CD的值;
,求AB+CD的值;
(3)若![]() 为a,
为a,![]() 为b,
为b,![]() 为c,求证:a+b=c.
为c,求证:a+b=c.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中反比例函数y=![]() 的图象经过点P(4,3)和点B(m,n)(其中0<m<4),作BA⊥x轴于点A,连接PA、OB,过P、B两点作直线PB,且S△AOB=S△PAB
的图象经过点P(4,3)和点B(m,n)(其中0<m<4),作BA⊥x轴于点A,连接PA、OB,过P、B两点作直线PB,且S△AOB=S△PAB
(1)求反比例函数的解析式;
(2)求点B的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC放在以O为原点的平面直角坐标系中,A(3,0),C(0,2),点E是AB的中点,点F在BC边上,且CF=1,若M为x轴上的动点,N为y轴上的动点,则四边形MNFE的周长最小值是_____.
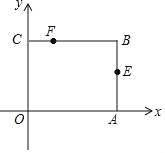
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】婷婷在发现一个门环的示意图如图所示.图中以正六边形ABCDEF的对角线AC的中点O为圆心,OB为半径作⊙O,AQ切⊙O于点P,并交DE于点Q,若AQ=12![]() cm,则该圆的半径为_____cm.
cm,则该圆的半径为_____cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com