
【题目】如图,两条射线BA//CD,PB和PC分别平分∠ABC和∠DCB,AD过点P,分别交AB,CD与点A,D.
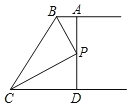
(1)求∠BPC的度数;
(2)若![]() ,求AB+CD的值;
,求AB+CD的值;
(3)若![]() 为a,
为a,![]() 为b,
为b,![]() 为c,求证:a+b=c.
为c,求证:a+b=c.
【答案】(1)90°;(2)4;(3)证明见解析
【解析】
(1)根据角平分线定义和平行线的性质,可得∠PBC+∠PCB的值,于是可求∠BPC的值;
(2)在△ABP,△PCD和△BCP中,利用特殊角在直角三角形中的边关系可求AB+CD的值.
(3)利用角平分线性质作垂直证明全等,通过割法获得面积关系.
(1)∵BA∥CD,∴∠ABC+∠BCD=180°.
∵PB和PC分别平分∠ABC和∠DCB,∴∠PBC![]() ∠ABC,∠PCB
∠ABC,∠PCB![]() ∠BCD,∴∠PBC+∠PCB
∠BCD,∴∠PBC+∠PCB![]() (∠ABC+∠BCD)=90°,∴∠BPC=90°;
(∠ABC+∠BCD)=90°,∴∠BPC=90°;
(2)若∠BCD=60°,BP=2,∴∠ABC=180°-60°=120°,∠PCD![]() ∠BCD=30°,∴∠ABP
∠BCD=30°,∴∠ABP![]() ∠ABC=60°.
∠ABC=60°.
在Rt△ABP中,BP=2,AB=1.在Rt△BCP中,CP=2![]() .在Rt△PCD中,PD
.在Rt△PCD中,PD![]() ,CD=3,∴AB+CD=4.
,CD=3,∴AB+CD=4.
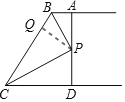
(3)如图,作PQ⊥BC.
∵∠ABP=∠QBP,∠BAP=∠BQP,BP=BP.
∴△ABP≌△BQP(AAS).
同理△PQC≌△PCD(AAS),∴S△BCP=S△BPQ+S△PQC=S△ABP+S△PCD,∴a+b=c.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
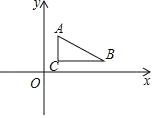
【题目】已知,如图,A点坐标是(1,3),B点坐标是(5,1),C点坐标是(1,1)
(1)求△ABC的面积是____;
(2)求直线AB的表达式;
(3)一次函数y=kx+2与线段AB有公共点,求k的取值范围;
(4)y轴上有一点P且△ABP与△ABC面积相等,则P点坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
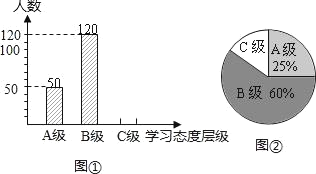
【题目】2011年,陕西西安被教育部列为“减负”工作改革试点地区.学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近80000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6 000元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
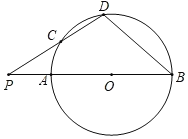
【题目】如图,AB为![]() 的直径,P为BA延长线上的一点,D在
的直径,P为BA延长线上的一点,D在![]() 上(不与点A,点B重合),连结PD交
上(不与点A,点B重合),连结PD交![]() 于点C,且PC=OB.设
于点C,且PC=OB.设![]() ,下列说法正确的是( )
,下列说法正确的是( )
A. 若![]() ,则
,则![]()
B. 若![]() ,则
,则![]()
C. 若![]() ,则
,则![]()
D. 若![]() ,则
,则![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“学雷锋、树新风、做文明中学生”号召,某校开展了志愿者服务活动,活动项目有“戒毒宣传”、“文明交通岗”、“关爱老人”、“义务植树”、“社区服务”等五项,活动期间,随机抽取了部分学生对志愿者服务情况进行调查,结果发现,被调查的每名学生都参与了活动,最少的参与了1项,最多的参与了5项,根据调查结果绘制了如图所示不完整的折线统计图和扇形统计图.
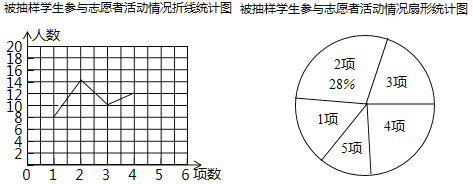
(1)被随机抽取的学生共有多少名?
(2)在扇形统计图中,求活动数为3项的学生所对应的扇形圆心角的度数,并补全折线统计图;
(3)该校共有学生2000人,估计其中参与了4项或5项活动的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《如果想毁掉一个孩子,就给他一部手机!》这是2017年微信圈一篇热传的文章.国际上,法国教育部宣布从 2018 年9月新学期起小学和初中禁止学生使用手机.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的 统计图,已知“查资料”的人数是 40人.请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的百分比为______,圆心角度数是______度;
(2)补全条形统计图;
(3)该校共有学生2100人,估计每周使用手机时间在2 小时以上(不含2小时)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
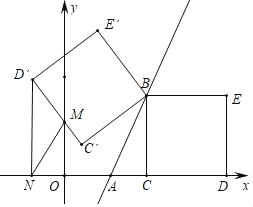
【题目】如图,在平面直角坐标系中,常数b<0,m>0,点A、B的坐标分别为(﹣![]() ,0)、(m,2m+b),正方形BCDE的顶点C、D分别在x轴的正半轴上.
,0)、(m,2m+b),正方形BCDE的顶点C、D分别在x轴的正半轴上.
(1)直接写出点D和点E的坐标(用含b、m的代数式表示);
(2)求![]() 的值;
的值;
(3)正方形BC′D′E′和正方形BCDE关于直线AB对称,点C′、D′、E′分别是点C、D、E的对称点,C′D′交y轴于点M,D′N⊥x轴,垂足为N,连接MN.
①若点N和点A关于y轴对称,求证:MN=MD′;
②若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雾霾是对大气中各种悬浮颗粒物含量超标的笼统表述,雾霾的主要危害可归纳为两种:一是对人体产生危害,二是对交通产生危害.雾霾天气是一种大气污染状态,成都市区冬天雾霾天气比较严重,很多家庭兴起了为家里添置“空气清洁器”的热潮,为此,我市某商场根据民众健康要,代理销售某种进价为600元/台的家用“空气清洁器”.经过市场销售后发现:在一个月内,当售价是700元/台时,可售出350台,且售价每提高10元,就会少售出5台.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;
(2)请计算当售价x(元台)定为多少时,该商场每月销售这种“空气清洁器”所获得的利润W(元)最大?最大利润是多少?
(3)若政府计划遴选部分商场,将销售“空气清洁器”纳入民生工程项目,规定:每销售一台“空气淸洁器”,财政补贴商家200元,但销售利润不能高于进价的25%,请问:该商场想获取最大利润,是否参与竞标此民生工程项目?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com