
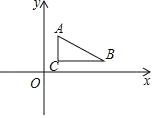
【题目】已知,如图,A点坐标是(1,3),B点坐标是(5,1),C点坐标是(1,1)
(1)求△ABC的面积是____;
(2)求直线AB的表达式;
(3)一次函数y=kx+2与线段AB有公共点,求k的取值范围;
(4)y轴上有一点P且△ABP与△ABC面积相等,则P点坐标是_____.
【答案】(1)4;(2)y=﹣![]() x+
x+![]() ;(3)0<k≤1或﹣
;(3)0<k≤1或﹣![]() ≤k<0;(4)(0,
≤k<0;(4)(0,![]() )或(0,
)或(0,![]() ).
).
【解析】
(1)根据A、B、C三点的坐标可得AC=3﹣1=2,BC=5﹣1=4,∠C=90°,再利用三角形面积公式列式计算即可;
(2)设直线AB的表达式为y=kx+b.将A(1,3),B(5,1)代入,利用待定系数法即可求解;
(3)由于y=kx+2是一次函数,所以k≠0,分两种情况进行讨论:①当k>0时,求出y=kx+2过A(1,3)时的k值;②当k<0时,求出y=kx+2过B(5,1)时的k值,进而求解即可;
(4)过C点作AB的平行线,交y轴于点P,根据两平行线间的距离相等,可知△ABP与△ABC是同底等高的两个三角形,面积相等.根据直线平移k值不变可设直线CP的解析式为y=﹣![]() x+n,将C点坐标代入,求出直线CP的解析式,得到P点坐标;再根据到一条直线距离相等的直线有两条,可得另外一个P点坐标.
x+n,将C点坐标代入,求出直线CP的解析式,得到P点坐标;再根据到一条直线距离相等的直线有两条,可得另外一个P点坐标.
解:(1)∵A点坐标是(1,3),B点坐标是(5,1),C点坐标是(1,1),
∴AC=3﹣1=2,BC=5﹣1=4,∠C=90°,
∴S△ABC=![]() ACBC=
ACBC=![]() ×2×4=4.
×2×4=4.
故答案为4;
(2)设直线AB的表达式为y=kx+b.
∵A点坐标是(1,3),B点坐标是(5,1),
∴![]() ,解得
,解得 ,
,
∴直线AB的表达式为y=﹣![]() x+
x+![]() ;
;
(3)当k>0时,y=kx+2过A(1,3)时,
3=k+2,解得k=1,
∴一次函数y=kx+2与线段AB有公共点,则0<k≤1;
当k<0时,y=kx+2过B(5,1),
1=5k+2,解得k=﹣![]() ,
,
∴一次函数y=kx+2与线段AB有公共点,则﹣
综上,满足条件的k的取值范围是0<k≤1或﹣![]() ≤k<0;
≤k<0;
(4)过C点作AB的平行线,交y轴于点P,此时△ABP与△ABC是同底等高的两个三角形,所以面积相等.
设直线CP的解析式为y=﹣![]() x+n,
x+n,
∵C点坐标是(1,1),
∴1=﹣![]() +n,解得n=
+n,解得n=![]() ,
,
∴直线CP的解析式为y=﹣![]() x+
x+![]() ,
,
∴P(0,![]() ).
).
设直线AB:y=﹣![]() x+
x+![]() 交y轴于点D,则D(0,
交y轴于点D,则D(0,![]() ).
).
将直线AB向上平移![]() ﹣
﹣![]() =2个单位,得到直线y=﹣
=2个单位,得到直线y=﹣![]() x+
x+![]() ,与y轴交于点P′,此时△ABP′与△ABP是同底等高的两个三角形,所以△ABP与△ABC面积相等,易求P′(0,
,与y轴交于点P′,此时△ABP′与△ABP是同底等高的两个三角形,所以△ABP与△ABC面积相等,易求P′(0,![]() ).
).
综上所述,所求P点坐标是(0,![]() )或(0,
)或(0,![]() ).
).
故答案为(0,![]() )或(0,
)或(0,![]() ).
).



 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】解决问题,一辆货车从超市出发,向东走了3千米到达小彬家,继续走2.5千米到达小颖家,然后向西走了10千米到达小明家,最后回到超市.
(1)以超市为原点,以向东的方向为正方向,用1个单位长度表示1千米,在数轴上表示出小明家.
(2)小明家距小彬家多远?
(3)货车一共行驶的多少千米?
(4)货车每千米耗油0.2升,这次共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①有两个角和第三个角的平分线对应相等的两个三角形全等;②有两条边和第三条边上的中线对应相等的两个三角形全等;③有两条边和第三条边上的高对应相等的两个三角形全等.其中正确的是( )
A. ①② B. ②③ C. ①③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
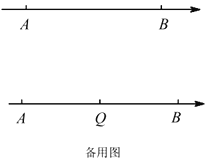
【题目】如图,数轴上点![]() ,
,![]() 表示的数
表示的数![]() ,
,![]() 满足
满足![]() ,点
,点![]() 为线段
为线段![]() 上一点(不与
上一点(不与![]() ,
,![]() 重合),
重合),![]() ,
,![]() 两点分别从
两点分别从![]() ,
,![]() 同时向数轴正方向移动,点
同时向数轴正方向移动,点![]() 运动速度为每秒2个单位长度,点
运动速度为每秒2个单位长度,点![]() 运动速度为每秒3个单位长度,设运动时间为
运动速度为每秒3个单位长度,设运动时间为![]() 秒(
秒(![]() ).
).
(1)直接写出![]() ______,
______,![]() ______;
______;
(2)若![]() 点表示的数是0.
点表示的数是0.
①![]() ,则
,则![]() 的长为______(直接写出结果);
的长为______(直接写出结果);
②点![]() ,
,![]() 在移动过程中,线段
在移动过程中,线段![]() ,
,![]() 之间是否存在某种确定的数量关系,判断并说明理由;
之间是否存在某种确定的数量关系,判断并说明理由;
(3)点![]() ,
,![]() 均在线段
均在线段![]() 上移动,若
上移动,若![]() ,且
,且![]() 到线段
到线段![]() 的中点
的中点![]() 的距离为3,请求出符合条件的点
的距离为3,请求出符合条件的点![]() 表示的数.
表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,现有一张边长为4的正方形纸片![]() ,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.
,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于三角函数有如下公式:sin(α+β)=sinαcosβ+cosαsinβ,sin(α﹣β)=sinαcosβ﹣cosαsinβ
cos(α+β)=cosαcosβ﹣sinαsinβ,cos(α﹣β)=cosαcosβ+sinαsinβ
tan(α+β)=![]() (1﹣tanαtanβ≠0)
(1﹣tanαtanβ≠0)
tan(α﹣β)=![]() (1+tanαtanβ≠0)
(1+tanαtanβ≠0)
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值.
如:tan105°=tan(45°+60°)=![]()
根据上面的知识,你可以选择适当的公式解决下面问题:
如图,两座建筑物AB和DC的水平距离BC为24米,从点A测得点D的俯角α=15°,测得点C的俯角β=75°,求建筑物CD的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为边AB上一点,连结DE,将ABCD沿DE翻折,使点A的对称点F落在CD上,连结EF.
(1)求证:四边形ADFE是菱形.
(2)若∠A=60°,AE=2BE=2.求四边形BCDE的周长.
小强做第(1)题的步骤
解:①由翻折得,AD=FD,AE=FE.
②∵AB∥CD.
③∴∠AED=∠FDE.
④∴∠AED=∠ADE
⑤∴AD=AE
⑥∴AD=AE=EF=FD
∴四边形ADFE是菱形.
(1)小强解答第(1)题的过程不完整,请将第(1)题的解答过程补充完整(说明在哪一步骤,补充什亻么条件或结论)
(2)完成题目中的第(2)小题.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCD的边BC在x轴的正半轴上,点B在点C的左侧,直线y=kx经过点A(2,2)和点P,且OP=4![]() ,将直线y=kx沿y轴向下平移得到直线y=kx+b,若点P落在矩形ABCD的内部,则b的取值范围是( )
,将直线y=kx沿y轴向下平移得到直线y=kx+b,若点P落在矩形ABCD的内部,则b的取值范围是( )

A. 0<b<2 B. -2<b<0 C. -4<b<2 D. -4<b<-2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com