
ΓΨΧβΡΩΓΩΙΊ”Ύ»ΐΫ«Κ· ΐ”–»γœ¬ΙΪ ΫΘΚsinΘ®ΠΝ+Π¬Θ©=sinΠΝcosΠ¬+cosΠΝsinΠ¬Θ§sinΘ®ΠΝ©¹Π¬Θ©=sinΠΝcosΠ¬©¹cosΠΝsinΠ¬
cosΘ®ΠΝ+Π¬Θ©=cosΠΝcosΠ¬©¹sinΠΝsinΠ¬Θ§cosΘ®ΠΝ©¹Π¬Θ©=cosΠΝcosΠ¬+sinΠΝsinΠ¬
tanΘ®ΠΝ+Π¬Θ©=![]() Θ®1©¹tanΠΝtanΠ¬ΓΌ0Θ©
Θ®1©¹tanΠΝtanΠ¬ΓΌ0Θ©
tanΘ®ΠΝ©¹Π¬Θ©=![]() Θ®1+tanΠΝtanΠ¬ΓΌ0Θ©
Θ®1+tanΠΝtanΠ¬ΓΌ0Θ©
άϊ”Ο’β–©ΙΪ ΫΩ…“‘ΫΪ“Μ–©≤Μ «ΧΊ βΫ«ΒΡ»ΐΫ«Κ· ΐΉΣΜ·ΈΣΧΊ βΫ«ΒΡ»ΐΫ«Κ· ΐά¥«σ÷ΒΘ°
»γΘΚtan105Γψ=tanΘ®45Γψ+60ΓψΘ©=![]()
ΗυΨί…œΟφΒΡ÷Σ ΕΘ§ΡψΩ…“‘―Γ‘ώ Β±ΒΡΙΪ ΫΫβΨωœ¬ΟφΈ ΧβΘΚ
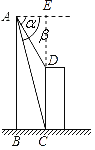
»γΆΦΘ§ΝΫΉυΫ®÷ΰΈοABΚΆDCΒΡΥ°ΤΫΨύάκBCΈΣ24ΟΉΘ§¥”ΒψA≤βΒΟΒψDΒΡΗ©Ϋ«ΠΝ=15ΓψΘ§≤βΒΟΒψCΒΡΗ©Ϋ«Π¬=75ΓψΘ§«σΫ®÷ΰΈοCDΒΡΗΏΕ»Θ°

ΓΨ¥πΑΗΓΩ48![]() m
m
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚ Ήœ»ΗυΨίΧβΡΩ÷–Ηχ≥ωΒΡΙΪ Ϋ«σ≥ωtan75ΓψΚΆtan15ΓψΒΡ÷ΒΘ§ΙΐAΉςAEΓΆCDΫΜCD―”≥ΛœΏ”ΎEΘ§ΗυΨίRtΓςAECΒΡ»ΐΫ«–ΈΚ· ΐ÷ΒΒΟ≥ωCEΒΡ÷ΒΘ§»ΜΚσΗυΨίRtΓςAEDΒΡ»ΐΫ«–ΈΚ· ΐ÷ΒΒΟ≥ωDEΒΡ≥ΛΕ»Θ§ΉνΚσΗυΨίCD=CEΘ≠DEΒΟ≥ω¥πΑΗΘ°
‘ΧβΫβΈωΘΚΫβΘΚΓΏtan75Γψ=tanΘ®30Γψ+45ΓψΘ©=![]() =
=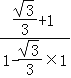 =2+
=2+![]() Θ§
Θ§
tan15Γψ=tanΘ®45Γψ©¹30ΓψΘ©=![]() =2©¹
=2©¹![]() Θ§
Θ§
»γΆΦΘ§ΙΐAΉςAEΓΆCDΫΜCD―”≥ΛœΏ”ΎEΘ§ ‘ΎRtΓςAEC÷–Θ§AE=BC=24mΘ§ΓœCAE=75ΓψΘ§
Γύtan75Γψ=![]() Θ§ ΓύCE=AEtan75Γψ=Θ®48+24
Θ§ ΓύCE=AEtan75Γψ=Θ®48+24![]() Θ©mΘ§
ȩmȧ
‘ΎRtΓςAED÷–Θ§tanΓœDAE=tan15Γψ=![]() Θ§ ΓύDE=AEtan15Γψ=48©¹24
Θ§ ΓύDE=AEtan15Γψ=48©¹24![]() mΘ§
mȧ
ΓύCD=CE©¹DE=48![]() mΘ°
mΘ°
¥πΘΚΫ®÷ΰΈοCDΒΡΗΏΕ» «48![]() mΘ°
mΘ°


 άΦΆΑΌΆ®÷ςΧεΩΈΧΟ–Γ―ßΩΈ ±Ά§≤Ϋ¥ο±ξœΒΝ–¥πΑΗ
άΦΆΑΌΆ®÷ςΧεΩΈΧΟ–Γ―ßΩΈ ±Ά§≤Ϋ¥ο±ξœΒΝ–¥πΑΗ άΦΆΑΌΆ®”≈ΝΖ≤βœΒΝ–¥πΑΗ
άΦΆΑΌΆ®”≈ΝΖ≤βœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΉ““ΝΫ»Υ‘»ΥΌ¥”Ά§“ΜΒΊΒψΒΫ1500ΟΉ¥ΠΒΡΆΦ ιΙίΩ¥ ιΘ§ΦΉ≥ωΖΔ5Ζ÷÷”ΚσΘ§“““‘50ΟΉ/Ζ÷ΒΡΥΌΕ»―ΊΆ§“Μ¬ΖœΏ––ΉΏΘ°…ηΦΉ““ΝΫ»ΥœύΨύsΘ®ΟΉΘ©Θ§ΦΉ––ΉΏΒΡ ±ΦδΈΣtΘ®Ζ÷Θ©Θ§sΙΊ”ΎtΒΡΚ· ΐΆΦœσΒΡ“Μ≤ΩΖ÷»γΆΦΥυ ΨΘ°œ¬Ν–Ϋα¬έ’ΐ»ΖΒΡΗω ΐ «Θ®ΓΓΓΓΘ©
Θ®1Θ©tΘΫ5 ±Θ§sΘΫ150ΘΜΘ®2Θ©tΘΫ35 ±Θ§sΘΫ450ΘΜΘ®3Θ©ΦΉΒΡΥΌΕ» «30ΟΉ/Ζ÷ΘΜΘ®4Θ©tΘΫ12.5 ±Θ§sΘΫ0Θ°

A. 1ΗωB. 2ΗωC. 3ΗωD. 4Ηω
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§’ΐΖΫ–ΈOABCΒΡΕΞΒψA‘Ύy÷α’ΐΑκ÷α…œΘ§ΕΞΒψC‘Ύx÷α’ΐΑκ÷α…œΘ§≈ΉΈοœΏ![]() Θ®a<0Θ©ΒΡΕΞΒψΈΣDΘ§«“Ψ≠ΙΐΒψAΓΔBΘ°»τΓςABDΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§‘ρaΒΡ÷ΒΈΣ___________Θ°
Θ®a<0Θ©ΒΡΕΞΒψΈΣDΘ§«“Ψ≠ΙΐΒψAΓΔBΘ°»τΓςABDΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§‘ρaΒΡ÷ΒΈΣ___________Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§AΘ®©¹3Θ§©¹4Θ©Θ§BΘ®0Θ§©¹2Θ©Θ°
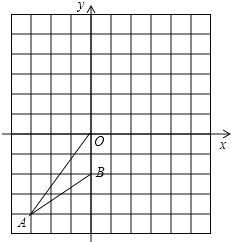
Θ®1Θ©ΓςOAB»ΤOΒψ–ΐΉΣ180ΓψΒΟΒΫΓςOA1B1Θ§«κΜ≠≥ωΓςOA1B1Θ§≤Δ–¥≥ωA1Θ§B1ΒΡΉχ±ξΘΜ
Θ®2Θ©≈–Εœ“‘AΘ§BΘ§A1Θ§B1ΈΣΕΞΒψΒΡΥΡ±Ώ–ΈΒΡ–ΈΉ¥Θ§≤ΔΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
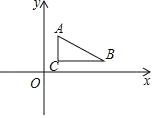
ΓΨΧβΡΩΓΩ“―÷ΣΘ§»γΆΦΘ§AΒψΉχ±ξ «(1Θ§3)Θ§BΒψΉχ±ξ «(5Θ§1)Θ§CΒψΉχ±ξ «(1Θ§1)
(1)«σΓςABCΒΡΟφΜΐ «____ΘΜ
(2)«σ÷±œΏABΒΡ±μ¥ο ΫΘΜ
(3)“Μ¥ΈΚ· ΐyΘΫkx+2”κœΏΕΈAB”–ΙΪΙ≤ΒψΘ§«σkΒΡ»Γ÷ΒΖΕΈßΘΜ
(4)y÷α…œ”–“ΜΒψP«“ΓςABP”κΓςABCΟφΜΐœύΒ»Θ§‘ρPΒψΉχ±ξ «_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΝΔΕ®Χχ‘Ε «Χε”ΐ÷–ΩΦ―ΓΩΦœνΡΩ÷°“ΜΘ§Χε”ΐΩΈ…œάœ ΠΦ«¬ΦΝΥΡ≥Ά§―ßΒΡ“ΜΉιΝΔΕ®Χχ‘Ε≥…Φ®»γ±μΘΚ
≥…Φ®Θ®mΘ© | 2.3 | 2.4 | 2.5 | 2.4 | 2.4 |
‘ρœ¬Ν–ΙΊ”Ύ’βΉι ΐΨίΒΡΥΒΖ®Θ§’ΐ»ΖΒΡ «Θ®ΓΓΓΓΘ©
A.÷Ύ ΐ «2.3B.ΤΫΨυ ΐ «2.4
C.÷–ΈΜ ΐ «2.5D.ΖΫ≤ν «0.01
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈ Χβ«ιΨ≥
–ΓΟςΚΆ–ΓάωΙ≤Ά§ΧΫΨΩ“ΜΒά ΐ―ßΧβΘΚ
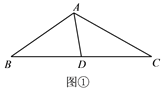
»γΆΦΔΌΘ§‘ΎΓςABC÷–Θ§ΒψD «±ΏBCΒΡ÷–ΒψΘ§ΓœBAD=65ΓψΘ§ΓœDAC=50ΓψΘ§AD=2Θ§
«σACΘ°
ΧΫΥςΖΔœ÷
–ΓΟςΒΡΥΦ¬Ζ «ΘΚ―”≥ΛAD÷ΝΒψEΘ§ ΙDE=ADΘ§ΙΙ‘λ»ΪΒ»»ΐΫ«–ΈΘ°
–ΓάωΒΡΥΦ¬Ζ «ΘΚΙΐΒψCΉςCEΓΈABΘ§ΫΜADΒΡ―”≥ΛœΏ”ΎΒψEΘ§ΙΙ‘λ»ΪΒ»»ΐΫ«–ΈΘ°
―Γ‘ώ–ΓΟςΓΔ–ΓάωΤδ÷–“Μ»ΥΒΡΖΫΖ®ΫβΨωΈ Χβ«ιΨ≥÷–ΒΡΈ ΧβΘ°
άύ±»”Π”Ο
»γΆΦΔΎΘ§‘ΎΥΡ±Ώ–ΈABCD÷–Θ§Ε‘Ϋ«œΏACΓΔBDœύΫΜ”ΎΒψOΘ§ΒψO «BDΒΡ÷–ΒψΘ§
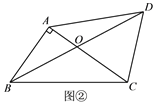
ABΓΆACΘ°»τΓœCAD=45ΓψΘ§ΓœADC=67.5ΓψΘ§AO=2Θ§‘ρBCΒΡ≥ΛΈΣ___________Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ2019Ρξ…νέΎ –¥¥Ϋ®ΈΡΟς≥« –ΤΎΦδΘ§Ρ≥«χΫΧ”ΐΨ÷ΈΣΝΥΝΥΫβ»Ϊ«χ÷–―ß…ζΕ‘ΩΈΆβΧε”ΐ‘ΥΕ·œνΡΩΒΡœ≤ΜΕ≥ΧΕ»Θ§ΥφΜζ≥ι»ΓΝΥΡ≥–ΘΑΥΡξΦΕ≤ΩΖ÷―ß…ζΫχ––Έ ΨμΒς≤ιΘ®ΟΩ»Υœό―Γ“Μ÷÷Χε”ΐ‘ΥΕ·œνΡΩΘ©.»γΆΦ «’ϊάμ ΐΨίΚσΜφ÷ΤΒΡΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ§«κΡψΗυΨίΆΦ÷–ΧαΙ©ΒΡ–≈œΔΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ


Θ®1Θ©’β¥ΈΜνΕ·“ΜΙ≤Βς≤ιΝΥ Οϊ―ß…ζΘΜ
Θ®2Θ©‘Ύ…»–ΈΆ≥ΦΤΆΦ÷–Θ§ΓΑΧχ…ΰΓ±Υυ‘Ύ…»–Έ‘≤–ΡΫ«Β»”Ύ Ε»ΘΜ
Θ®3Θ©≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘΜ
Θ®4Θ©»τΗΟ–Θ”–―ß…ζ2000»ΥΘ§ «κΡψΙάΦΤΗΟ–Θœ≤ΜΕΓΑΉψ«ρΓ±ΒΡ―ß…ζ‘Φ”– .
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΒψΘ®aΘ§y1Θ©Θ®a+2Θ§y2Θ©ΕΦ‘ΎΖ¥±»άΐΚ· ΐyΘΫ![]() Θ®kΘΦ0Θ©ΒΡΆΦœσ…œΘ§»τy1ΘΨy2Θ§‘ρaΒΡ»Γ÷ΒΖΕΈß «_____Θ°
Θ®kΘΦ0Θ©ΒΡΆΦœσ…œΘ§»τy1ΘΨy2Θ§‘ρaΒΡ»Γ÷ΒΖΕΈß «_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com