
【题目】如图,在ABCD中,E为边AB上一点,连结DE,将ABCD沿DE翻折,使点A的对称点F落在CD上,连结EF.
(1)求证:四边形ADFE是菱形.
(2)若∠A=60°,AE=2BE=2.求四边形BCDE的周长.
小强做第(1)题的步骤
解:①由翻折得,AD=FD,AE=FE.
②∵AB∥CD.
③∴∠AED=∠FDE.
④∴∠AED=∠ADE
⑤∴AD=AE
⑥∴AD=AE=EF=FD
∴四边形ADFE是菱形.
(1)小强解答第(1)题的过程不完整,请将第(1)题的解答过程补充完整(说明在哪一步骤,补充什亻么条件或结论)
(2)完成题目中的第(2)小题.

【答案】(1)见解析;(2)四边形BCDE的周长为8.
【解析】
(1)由题意可知,第一步补充∠ADE=∠FDE.
(2)由平行四边形的性质和菱形的性质可得,BE,BC,CD,DE的长度,即可求四边形BCDE的周长
解:(1)①由翻折得,AD=FD,AE=FE.(补充∠ADE=∠FDE)
②∵AB∥CD
③∴∠AED=∠FDE.
④∴∠AED=∠ADE
⑤∴AD=AE
⑥∴AD=AE=EF=FD
∴四边形ADFE是菱形.
(2)∵AE=2BE=2
∴BE=1
∴AB=CD=3
∵AD=AE,∠A=60°∴△ADE是等边三角形∴AD=DE=2
∴AD=BC=2
∴四边形BCDE的周长=BE+DE+CD+BC=1+2+3+2=8.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
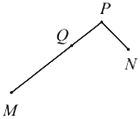
【题目】如图,有公共端点![]() 的两条线段
的两条线段![]() ,
,![]() 组成一条折线
组成一条折线![]() ,若该折线
,若该折线![]() 上一点
上一点![]() 把这条折线分成相等的两部分,我们把这个点
把这条折线分成相等的两部分,我们把这个点![]() 叫做这条折线的“折中点”.已知点
叫做这条折线的“折中点”.已知点![]() 是折线
是折线![]() 的“折中点”,点
的“折中点”,点![]() 为线段
为线段![]() 的中点,
的中点,![]() ,
,![]() ,则线段
,则线段![]() 的长为______.
的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
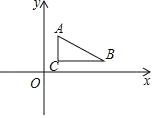
【题目】已知,如图,A点坐标是(1,3),B点坐标是(5,1),C点坐标是(1,1)
(1)求△ABC的面积是____;
(2)求直线AB的表达式;
(3)一次函数y=kx+2与线段AB有公共点,求k的取值范围;
(4)y轴上有一点P且△ABP与△ABC面积相等,则P点坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境
小明和小丽共同探究一道数学题:
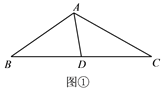
如图①,在△ABC中,点D是边BC的中点,∠BAD=65°,∠DAC=50°,AD=2,
求AC.
探索发现
小明的思路是:延长AD至点E,使DE=AD,构造全等三角形.
小丽的思路是:过点C作CE∥AB,交AD的延长线于点E,构造全等三角形.
选择小明、小丽其中一人的方法解决问题情境中的问题.
类比应用
如图②,在四边形ABCD中,对角线AC、BD相交于点O,点O是BD的中点,
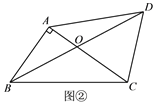
AB⊥AC.若∠CAD=45°,∠ADC=67.5°,AO=2,则BC的长为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:![]() )
)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
(1)求收工时,检修小组在![]() 地的何方向?距离
地的何方向?距离![]() 地多远?
地多远?
(2)在第几次纪录时距![]() 地最远?
地最远?
(3)若汽车行驶每千米耗油0.4升,问从![]() 地出发,检修结束后再回到
地出发,检修结束后再回到![]() 地共耗油多少升?
地共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年深圳市创建文明城市期间,某区教育局为了了解全区中学生对课外体育运动项目的喜欢程度,随机抽取了某校八年级部分学生进行问卷调查(每人限选一种体育运动项目).如图是整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:


(1)这次活动一共调查了 名学生;
(2)在扇形统计图中,“跳绳”所在扇形圆心角等于 度;
(3)补全条形统计图;
(4)若该校有学生2000人, 请你估计该校喜欢“足球”的学生约有 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:如图(1),已知正方形ABCD和等腰直角△EBF,点E在正方形BC边上,点F在AB边的延长线上,∠EBF=90°,连结AE、CF.
易证:∠AEB=∠CFB(不需要证明).
探究:如图(2),已知正方形ABCD和等腰直角△EBF,点E在正方形ABCD内部,点F在正方形ABCD外部,∠EBF=90°,连结AE、CF.
求证:∠AEB=∠CFB
应用:如图(3),在(2)的条件下,当A、E、F三点共线时,连结CE,若AE=1,EF=2,则CE=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
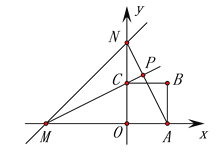
【题目】如图直线y=x+2分别与x轴,y轴交于点M、N,边长为1的正方形OABC的一个顶点O在坐标系原点,直线AN与MC交于点P,若正方形绕点O旋转一周,则点P到点(0,1)长度的最小值是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y1=![]() 的图象与函数y2=kx+b的图象交于点A(﹣1,a)B(﹣8+a,1)
的图象与函数y2=kx+b的图象交于点A(﹣1,a)B(﹣8+a,1)

(1)求函数y=![]() 和y=kx+b的表达式;
和y=kx+b的表达式;
(2)观察图象,直接写出不等式![]() <kx+b的解.
<kx+b的解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com