
【题目】如图,有公共端点![]() 的两条线段
的两条线段![]() ,
,![]() 组成一条折线
组成一条折线![]() ,若该折线
,若该折线![]() 上一点
上一点![]() 把这条折线分成相等的两部分,我们把这个点
把这条折线分成相等的两部分,我们把这个点![]() 叫做这条折线的“折中点”.已知点
叫做这条折线的“折中点”.已知点![]() 是折线
是折线![]() 的“折中点”,点
的“折中点”,点![]() 为线段
为线段![]() 的中点,
的中点,![]() ,
,![]() ,则线段
,则线段![]() 的长为______.
的长为______.
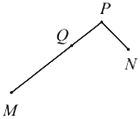
【答案】4或16
【解析】
分两种情况:点D在线段AC上,由E为线段AC中点,CE=5,得到AC=2CE=10,于是得到AD=AC-CD=7,根据线段的和差即可得到结论;点D在线段BC上,由E为线段AC中点,CE=4,得到AC=2CE=10,于是得到AD=AC+CD=13,根据线段的和差即可得到结论.
分两种情况:①点D在线段AC上,如图所示,
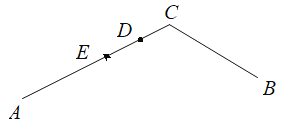
∵E为线段AC中点,CE=5,如图所示,
∴AC=2CE=10,
∵CD=3,
∴AD=AC-CD=7,
∵BD=AD=7,
∴BC=7-3=4;
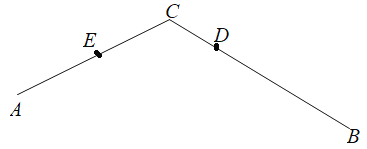
②点D在线段BC上,
∵E为线段AC中点,CE=5,
∴AC=2CE=10,
∵CD=3,
∴AD=AC+CD=13,
∵BD=AD=13,
∴BC=13+3=16.
故答案为:4或16.


科目:初中数学 来源: 题型:
【题目】“知识改变命运,科技繁荣祖国”.我市中小学每年都要举办一届科技运动会.下图为我市某校2009年参加科技运动会航模比赛(包括空模、海模、车模、建模四个类别)的参赛人数统计图:
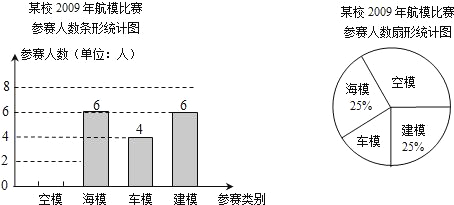
(1)该校参加车模、建模比赛的人数分别是 人和 人;
(2)该校参加航模比赛的总人数是 人,空模所在扇形的圆心角的度数是 °,并把条形统计图补充完整;(温馨提示:作图时别忘了用0.5毫米及以上的黑色签字笔涂黑)
(3)从全市中小学参加航模比赛选手中随机抽取80人,其中有32人获奖.今年我市中小学参加航模比赛人数共有2485人,请你估算今年参加航模比赛的获奖人数约是多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解决问题,一辆货车从超市出发,向东走了3千米到达小彬家,继续走2.5千米到达小颖家,然后向西走了10千米到达小明家,最后回到超市.
(1)以超市为原点,以向东的方向为正方向,用1个单位长度表示1千米,在数轴上表示出小明家.
(2)小明家距小彬家多远?
(3)货车一共行驶的多少千米?
(4)货车每千米耗油0.2升,这次共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“全民读书月”活动中,小明调查了班级里40名同学本学期计划购买课外书的花费情况,并将结果绘制成如图所示的统计图,请根据相关信息,解答下列问题:(直接填写结果)

(1)本次调查获取的样本数据的众数是 ;
(2)这次调查获取的样本数据的中位数是 ;
(3)若该校共有学生1000人,根据样本数据,估计本学期计划购买课外书花费50元的学生有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
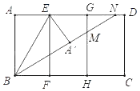
【题目】如图,矩形纸片ABCD,AB=8,AE=EG=GD=4,AB∥EF∥GH.将矩形纸片沿BE折叠,得到△BA′E(点A折叠到A′处),展开纸片;再沿BA′折叠,折痕与GH,AD分别交于点M,N,然后将纸片展开.
(1)连接EM,证明A′M=MG;
(2)设A′M=MG=x,求x值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学完三角形的高后,小明对三角形与高线做了如下研究:如图,![]() 是
是![]() 中边
中边![]() 上的-点,过点
上的-点,过点![]() 、
、![]() 分别作、
分别作、![]() 、
、![]() 、
、![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() 、
、![]() ,由
,由![]() 与
与![]() 的面积之和等于
的面积之和等于![]() 的面积,有等量关系式:
的面积,有等量关系式:![]() .像这种利用同一平面图形的两种面积计算途径可以得出相关线段的数量关系式,从而用于解决数学问题的方法称为“等积法”,下面请尝试用这种方法解决下列问题.
.像这种利用同一平面图形的两种面积计算途径可以得出相关线段的数量关系式,从而用于解决数学问题的方法称为“等积法”,下面请尝试用这种方法解决下列问题.



图(1) 图(2)
(1)如图(1), 矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点,过点
上一点,过点![]() 作
作![]() ,
,![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() ,求
,求![]() 的值;
的值;
(2)如图(2),在![]() 中,角平分线
中,角平分线![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 分别作
分别作![]() 、
、![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() ,若
,若![]() ,
,![]() ,求四边形
,求四边形![]() 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①有两个角和第三个角的平分线对应相等的两个三角形全等;②有两条边和第三条边上的中线对应相等的两个三角形全等;③有两条边和第三条边上的高对应相等的两个三角形全等.其中正确的是( )
A. ①② B. ②③ C. ①③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上点![]() ,
,![]() 表示的数
表示的数![]() ,
,![]() 满足
满足![]() ,点
,点![]() 为线段
为线段![]() 上一点(不与
上一点(不与![]() ,
,![]() 重合),
重合),![]() ,
,![]() 两点分别从
两点分别从![]() ,
,![]() 同时向数轴正方向移动,点
同时向数轴正方向移动,点![]() 运动速度为每秒2个单位长度,点
运动速度为每秒2个单位长度,点![]() 运动速度为每秒3个单位长度,设运动时间为
运动速度为每秒3个单位长度,设运动时间为![]() 秒(
秒(![]() ).
).
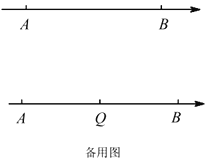
(1)直接写出![]() ______,
______,![]() ______;
______;
(2)若![]() 点表示的数是0.
点表示的数是0.
①![]() ,则
,则![]() 的长为______(直接写出结果);
的长为______(直接写出结果);
②点![]() ,
,![]() 在移动过程中,线段
在移动过程中,线段![]() ,
,![]() 之间是否存在某种确定的数量关系,判断并说明理由;
之间是否存在某种确定的数量关系,判断并说明理由;
(3)点![]() ,
,![]() 均在线段
均在线段![]() 上移动,若
上移动,若![]() ,且
,且![]() 到线段
到线段![]() 的中点
的中点![]() 的距离为3,请求出符合条件的点
的距离为3,请求出符合条件的点![]() 表示的数.
表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为边AB上一点,连结DE,将ABCD沿DE翻折,使点A的对称点F落在CD上,连结EF.
(1)求证:四边形ADFE是菱形.
(2)若∠A=60°,AE=2BE=2.求四边形BCDE的周长.
小强做第(1)题的步骤
解:①由翻折得,AD=FD,AE=FE.
②∵AB∥CD.
③∴∠AED=∠FDE.
④∴∠AED=∠ADE
⑤∴AD=AE
⑥∴AD=AE=EF=FD
∴四边形ADFE是菱形.
(1)小强解答第(1)题的过程不完整,请将第(1)题的解答过程补充完整(说明在哪一步骤,补充什亻么条件或结论)
(2)完成题目中的第(2)小题.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com