
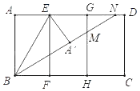
【题目】如图,矩形纸片ABCD,AB=8,AE=EG=GD=4,AB∥EF∥GH.将矩形纸片沿BE折叠,得到△BA′E(点A折叠到A′处),展开纸片;再沿BA′折叠,折痕与GH,AD分别交于点M,N,然后将纸片展开.
(1)连接EM,证明A′M=MG;
(2)设A′M=MG=x,求x值.
【答案】(1)见解析;(2)A′M=6﹣2![]() .
.
【解析】
(1)由翻折的性质得到A'E=EG,由矩形的性质好而其他条件得∠EGM=90°,从而得到Rt△EA'M≌Rt△EGM(HL),则A′M=MG;
(2)由已知条件,根据勾股定理得到BE的值,再由已知条件得到![]() ,设A′M=MG=x,从而得到x的值.
,设A′M=MG=x,从而得到x的值.
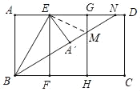
(1)连接EM,如图.
由折叠可知EA=EA',
∵AE=EG,∠EA'B=∠A=90°
∴A'E=EG,
∵四边形ABCD为矩形,AB∥EF∥GH,
∴∠EGM=90°
∴∠EGM=∠EA'M,
∴Rt△EA'M≌Rt△EGM(HL),
∴A′M=MG;
(2)∵AB=8,AE=4,
∴BE=![]() ,
,
∴EN=BE=![]() ,
,
∵AB∥EF∥GH,AE=EG=GD=4,AB=8,
∴![]() ,
,
设A′M=MG=x,
![]()
x=6﹣2![]() .
.


科目:初中数学 来源: 题型:
【题目】某淘宝店销售A,B两种商品,2018年8~12月每月销售数量的情况如图所示,在________月结束后,A![]() 商品的总销售数量大于B
商品的总销售数量大于B![]() 商品的总销售数量.
商品的总销售数量.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,有点![]() 、点
、点![]() .
.
(1)当A、B两点关于x轴对称时,求![]() 的面积;
的面积;
(2)若点A向上平移2个单位,再向右平移3个单位,得到点与点B重合,求A的坐标;
(3)当线段![]() 轴,且
轴,且![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
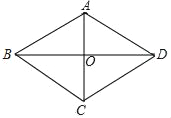
【题目】如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠BAO=∠DAO.
(1)求证:平行四边形ABCD是菱形;
(2)请添加一个条件使菱形ABCD为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
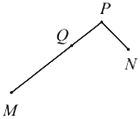
【题目】如图,有公共端点![]() 的两条线段
的两条线段![]() ,
,![]() 组成一条折线
组成一条折线![]() ,若该折线
,若该折线![]() 上一点
上一点![]() 把这条折线分成相等的两部分,我们把这个点
把这条折线分成相等的两部分,我们把这个点![]() 叫做这条折线的“折中点”.已知点
叫做这条折线的“折中点”.已知点![]() 是折线
是折线![]() 的“折中点”,点
的“折中点”,点![]() 为线段
为线段![]() 的中点,
的中点,![]() ,
,![]() ,则线段
,则线段![]() 的长为______.
的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形.请你参考这个作全等三角形的方法,解答下列问题:
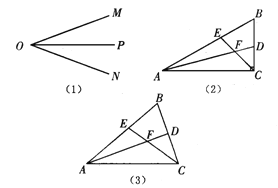
(1)如图(2),在△ABC中,∠ACB是直角,∠B=60°, AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你判断并写出FE与FD之间的数量关系;
(2)如图(3),在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,在(1)中所得结论是否仍然成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,以
,以![]() 为边长作等边
为边长作等边![]() ,过点
,过点![]() 作
作![]() 平行于
平行于![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,以
,以![]() 为边长作等边
为边长作等边![]() ,过点
,过点![]() 作
作![]() 平行于
平行于![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,以
,以![]() 为边长作等边
为边长作等边![]() ,…,则等边
,…,则等边![]() 的边长是______.
的边长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:![]() )
)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
(1)求收工时,检修小组在![]() 地的何方向?距离
地的何方向?距离![]() 地多远?
地多远?
(2)在第几次纪录时距![]() 地最远?
地最远?
(3)若汽车行驶每千米耗油0.4升,问从![]() 地出发,检修结束后再回到
地出发,检修结束后再回到![]() 地共耗油多少升?
地共耗油多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com