[题目]如图.在平面直角坐标系中.矩形ABCD的边BC在x轴的正半轴上.点B在点C的左侧.直线y=kx经过点A(2,2)和点P.且OP=4.将直线y=kx沿y轴向下平移得到直线y=kx+b.若点P落在矩形ABCD的内部.则b的取值范围是( ) A. 0＜b＜2 B. -2＜b＜0 C. -4＜b＜2 D. -4＜b＜-2 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，在平面直角坐标系中，矩形ABCD的边BC在x轴的正半轴上，点B在点C的左侧，直线y=kx经过点A（2,2）和点P，且OP=4，将直线y=kx沿y轴向下平移得到直线y=kx+b，若点P落在矩形ABCD的内部，则b的取值范围是（）

A. 0＜b＜2 B. －2＜b＜0 C. －4＜b＜2 D. －4＜b＜－2

【答案】D

【解析】解：如图作PE⊥AD于E交BC于F．∵直线y=kx经过点A（2，2），∴k=1，∴直线为y=x，设点P坐标（a，a）．∵OP=，∴a2+a2=32，∴a2=16．∵a＞0，∴a=4，∴点P坐标（4，4），点E（4，2），点F（4，0），把点E（4，2），点F（4，0）分别代入y=x+b中，得到b=﹣2或﹣4，∴点P落在矩形ABCD的内部，∴﹣4＜b＜﹣2．故选D．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

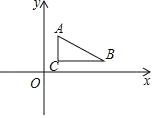
【题目】已知，如图，A点坐标是(1，3)，B点坐标是(5，1)，C点坐标是(1，1)

(1)求△ABC的面积是____；

(2)求直线AB的表达式；

(3)一次函数y＝kx+2与线段AB有公共点，求k的取值范围；

(4)y轴上有一点P且△ABP与△ABC面积相等，则P点坐标是_____．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】感知：如图（1），已知正方形ABCD和等腰直角△EBF，点E在正方形BC边上，点F在AB边的延长线上，∠EBF=90°，连结AE、CF．

易证：∠AEB=∠CFB（不需要证明）．

探究：如图（2），已知正方形ABCD和等腰直角△EBF，点E在正方形ABCD内部，点F在正方形ABCD外部，∠EBF=90°，连结AE、CF．

求证：∠AEB=∠CFB

应用：如图（3），在（2）的条件下，当A、E、F三点共线时，连结CE，若AE=1，EF=2，则CE=______．

查看答案和解析>>

科目：初中数学 来源： 题型：

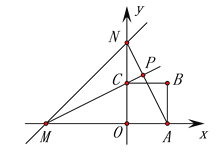
【题目】如图直线y=x+2分别与x轴，y轴交于点M、N，边长为1的正方形OABC的一个顶点O在坐标系原点，直线AN与MC交于点P，若正方形绕点O旋转一周，则点P到点（0,1）长度的最小值是___________.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，直线y1＝3x+4交x轴、y轴于点A、C，直线y2＝﹣x+4交x轴、y轴于点B、C，点P（m，2）是△ABC内部（包括边上）的一点，则m的最大值与最小值之差为（　　）

A.B.6C.D.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】点（a，y1）（a+2，y2）都在反比例函数y＝（k＜0）的图象上，若y1＞y2，则a的取值范围是_____．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】近年来，我国很多地区持续出现雾霾天气．某社区为了调查本社区居民对雾霾天气主要成因的认识情况，随机对该社区部分居民进行了问卷调查，要求居民从五个主要成因中只选择其中的一项，被调查居民都按要求填写了问卷．社区对调查结果进行了整理，绘制了如下不完整的统计图表．被调查居民选择各选项人数统计表

雾霾天气的主要成因	频数（人数）
A大气气压低，空气不流动	m
B地面灰尘大，空气湿度低	40
C汽车尾气排放	n
D工厂造成的污染	120
E其他	60