
����Ŀ�������ǶԴ����и������������ﺬ���������ͳ��������������ҪΣ���ɹ���Ϊ���֣�һ�Ƕ��������Σ�������ǶԽ�ͨ����Σ��������������һ�ִ�����Ⱦ״̬���ɶ������������������Ƚ����أ��ܶ��ͥ������Ϊ������������������������ȳ���Ϊ�ˣ�����ij�̳��������ڽ���Ҫ����������ij�ֽ���Ϊ600Ԫ/̨�ļ�����������������������г����ۺ��֣���һ�����ڣ����ۼ���700Ԫ/̨ʱ�����۳�350̨�����ۼ�ÿ���10Ԫ���ͻ����۳�5̨��
��1����ȷ����������y��̨�����ۼ�x��Ԫ/̨��֮��ĺ�����ϵʽ��
��2������㵱�ۼ�x��Ԫ̨����Ϊ����ʱ�����̳�ÿ���������������������������õ�����W��Ԫ�������������Ƕ��٣�
��3���������ƻ���ѡ�����̳������������������������������������Ŀ���涨��ÿ����һ̨�������[�����������������̼�200Ԫ�������������ܸ��ڽ��۵�25%�����ʣ����̳����ȡ��������Ƿ���뾺�������������Ŀ����˵�����ɣ�
���𰸡���1��![]() ����2����x��100ʱ��w��80000����3�����̳����ȡ���������뾺�������������Ŀ��
����2����x��100ʱ��w��80000����3�����̳����ȡ���������뾺�������������Ŀ��
��������
��1��������ã�y��350��![]() ��x��700����������⣻
��x��700����������⣻
��2��������ã�w��y��x��600����������⣻
��3��ÿ̨���������ܸ��ڽ��۵�25%����600����1+25%����750������x��750��������ã�w����700��![]() x����x��600+200������
x����x��600+200������![]() ��x��1400����x��400����x��750ʱ����x��750ʱ��ȡ�����ֵ��������⣮
��x��1400����x��400����x��750ʱ����x��750ʱ��ȡ�����ֵ��������⣮
��1��������ã�y��350��![]() ��x��700������
��x��700������![]() x+700��
x+700��
��2��������ã�w��y��x��600������![]() ��x��600����x��1400����
��x��600����x��1400����
��-![]() ��0���ʺ��������ֵ����x����
��0���ʺ��������ֵ����x����![]() ��100ʱ��w��80000��
��100ʱ��w��80000��
��3��ÿ̨���������ܸ��ڽ��۵�25%����600����1+25%����750������x��750��
������ã�w����700��![]() x����x��600+200������
x����x��600+200������![]() ��x��1400����x��400����
��x��1400����x��400����
x��750ʱ����x��750ʱ��ȡ�����ֵ����Ϊ��113750��80000��
�ʣ����̳����ȡ���������뾺�������������Ŀ��


 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=ax+b��ͼ���뷴��������![]() ��ͼ����C��D���㣬��x��y�ύ��B��A���㣬��tan��ABO=
��ͼ����C��D���㣬��x��y�ύ��B��A���㣬��tan��ABO=![]() ��OB=4��OE=2��
��OB=4��OE=2��
��1����һ�κ����Ľ���ʽ�ͷ����������Ľ���ʽ��
��2������OCD�������
��3������ͼ��ֱ��д��һ�κ�����ֵ���ڷ�����������ֵʱ���Ա���x��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵ�����һ���Ʒ��ÿ���ijɱ���50Ԫ��Ϊ�˺������ۣ�Ͷ���г��������������г����飬���۵�����100Ԫʱ��ÿ�����������50���������۵���ÿ����1Ԫ��ÿ��Ϳɶ��۳�5������Ҫ�����۵��۲��õ��ڳɱ���
��1�������۵���Ϊ70Ԫʱ��ÿ������������Ƕ��٣�
��2�����ÿ�����������y��Ԫ�������۵���x��Ԫ��֮��ĺ�����ϵʽ��������Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3���������ҵÿ����ܳɱ�������7000Ԫ����ô���۵���Ϊ����Ԫʱ��ÿ����������������������Ƕ��٣���ÿ����ܳɱ���ÿ���ijɱ���ÿ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �ֱ���������
�ֱ���������![]() �ı�
�ı�![]() ���е㣬��
���е㣬��![]() Ϊ����������
����������![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��

��1����֤��![]() ��
��
��2����![]() ����֤
����֤![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABCD�У�AB=6��AD=10������P�ӵ�D�������ڱ�DA����ÿ��1����λ���ٶ����A�˶�������CP������D����ֱ��PC�ĶԳƵ�E�����P���˶�ʱ��Ϊt(x)����P��E��B������ͬһֱ����ʱ��Ӧt��ֵΪ�� ����
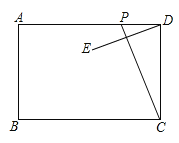
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�У���E��F��G��H�ֱ���AB��BC��CD��AD������AE=CG��AH=CF��

��1����֤���ı���EFGH��ƽ���ı��Σ�
��2�����AB=AD����AH=AE����֤���ı���EFGH�Ǿ��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ڽ��ڡ�O����BAD=90������E��BC���ӳ����ϣ��ҡ�DEC=��BAC��
��1����֤��DE�ǡ�O�����ߣ�
��2����AC��DE����AB=8��CE=2ʱ����AC�ij���
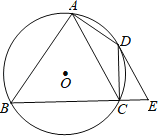
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y����![]() x+2��ͼ����x����һ��P��m��0����ת180�㣬���õ�ͼ����0����1������m��ֵΪ��������
x+2��ͼ����x����һ��P��m��0����ת180�㣬���õ�ͼ����0����1������m��ֵΪ��������
A.��2B.��1C.1D.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���ȫ�С���ֹ���սոѡ�������ijѧУ�����ˡ���ֹ���սոѣ�������������������Ϊ������ݽ�����. ������ί����������ͬѧ�ijɼ��������������²�������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ�������ͼ���ṩ����Ϣ������������⣺
������ ������Ϊx�֣� | Ƶ�� | �ٷֱ� |
60��x��70 | 8 | 20% |
70��x��80 | a | 30% |
80��x��90 | 16 | b% |
90��x��100 | 4 | 10% |
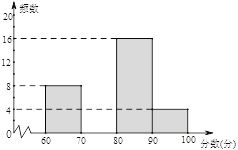
��1�����е�a�� ��b��������������
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3����������ͳ��ͼ�������ɼ��ֲ�������������70��x��80��Ӧ��Բ�ĽǵĶ����� ��
��4�������ɼ�������90�ֵ�4��ͬѧ��������2����ͬѧ��2��Ůͬѧ.ѧУ����4��ͬѧ�������ȡ2��ͬѧ���ܵ���̨���߲ɷã������б�����״ͼ�ķ��������ó鵽һ����ͬѧ��һ��Ůͬѧ�ĸ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com