
【题目】如图①,先把一矩形ABCD纸片上下对折,设折痕为MN;如图②,再把点B叠在折痕线MN上,得到Rt△ABE.过B点作PQ⊥MN,分别交EC、AD于点P、Q.

(1)求证:△PBE∽△QAB;
(2)在图②中,如果沿直线EB再次折叠纸片,点A能否叠在直线EC上?请说明理由;
(3)在(2)的条件下,若AB=3![]() ,求AE的长度.
,求AE的长度.
【答案】(1)见解析;(2)沿直线EB再次折叠纸片,点A能叠在直线EC上;(3)2![]()
【解析】
试题分析:(1)由题意可以得到∠BPE=∠AQB=90°,通过角的转化可以得到∠BEP=∠ABQ,从而可以得到△PBE∽△QAB;
(2)根据折叠的知识可以得到QB=PB,由第(1)问中的相似可以得到对应边成比例,通过转化可以得到△PBE∽△BAE,从而可以解答本题;
(3)由题意和第(2)问可以得到∠AEB=∠BEP=60°,∠ABE=90°,又因为AB=3![]() ,sin∠AEB=
,sin∠AEB=![]() ,从而可以得到AE的长度.
,从而可以得到AE的长度.
(1)证明:∵PQ⊥MN,BN∥EC∥AD,
∴∠BPE=∠AQB=∠PBN=∠NBQ=90°,
∴∠PBE+∠BEP=90°,
又∵∠PBE+∠ABQ=180°﹣∠ABE=180°﹣90°=90°,
∴∠BEP=∠ABQ,
在△PBE∽△QAB中
![]()
∴△PBE∽△QAB;
(2)点A能叠在直线EC上,
理由:∵△PBE∽△QAB,
∴![]() ,
,
∵由折叠可知,QB=PB,
∴![]() ,即
,即![]() ,
,
又∵∠ABE=∠BPE=90°,
∴△PBE∽△BAE,
∴∠AEB=∠PEB,
∴沿直线EB再次折叠纸片,点A能叠在直线EC上;
(3)解:由(2)可知,∠AEB=∠PEB,
而由折叠过程知:2∠AEB+∠PEB=180°,
∴∠AEB=∠PEB=60°,
在Rt△ABE中,sin∠AEB=![]() ,
,
∴AE=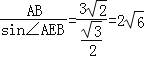 .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
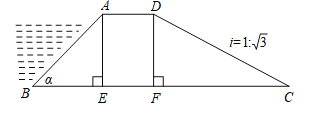
【题目】如图所示,某拦水大坝的横断面为梯形ABCD,AE、DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长AB=![]() 米,背水坡CD的坡度i=1:
米,背水坡CD的坡度i=1:![]() (i为DF与FC的比值),则背水坡CD的坡长为______米.
(i为DF与FC的比值),则背水坡CD的坡长为______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲班56人,其中身高在160厘米以上的男同学10人,身高在160厘米以上的女同学3人,乙班80人,其中身高在160厘米以上的男同学20人,身高在160厘米以上的女同学8人.如果想在两个班的160厘米以上的女生中抽出一个作为旗手,在哪个班成功的机会大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】①对角线互相垂直且相等的平行四边形是正方形;
②平行四边形、矩形、等边三角形、正方形既是中心对称图形,也是轴对称图形;
③旋转和平移都不改变图形的形状和大小;
④底角是45°的等腰梯形,高是h,则腰长是![]() h;
h;
⑤一组对边平行,另一组对边相等的四边形是平行四边形.
以上正确的命题是( )
A. ①②③④ B. ①②④ C. ①②③ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
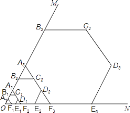
【题目】如图,∠MON=60°,作边长为1的正六边形A1B1C1D1E1F1,边A1B1、F1E1分别在射线OM、ON上,边C1D1所在的直线分别交OM、ON于点A2、F2, 以A2F2为边作正六边形A2B2C2D2E2F2, 边C2D2所在的直线分别交OM、ON于点A3、F3, 再以A3F3为边作正六边形A3B3C3D3E3F3, …,依此规律,经第4次作图后,点B4到ON的距离是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中装有3个带号码的球,球号分别为2,3,4,这些球除号码不同外其它均相同。甲、乙、两同学玩摸球游戏,游戏规则如下:
先由甲同学从中随机摸出一球,记下球号,并放回搅匀,再由乙同学从中随机摸出一球,记下球号。将甲同学摸出的球号作为一个两位数的十位上的数,乙同学的作为个位上的数。若该两位数能被4整除,则甲胜,否则乙胜.
问:这个游戏公平吗?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
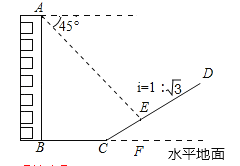
【题目】(8分)如图,一楼房AB后有一假山,其坡度为![]() ,山坡坡面上E点处有一休息亭,测的假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测的假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】袋子中装有3个带号码的球,球号分别是2,3,5,这些球除号码不同外其他均相同.
(1)从袋中随机摸出一个球,求恰好是3号球的概率;
(2)从袋中随机摸出一个球,再从剩下的球中随机摸出一个球,用树形图列出所有可能出现的结果,并求两次摸出球的号码之和为5的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com