
| A. | ∠A=∠D时,两三角形相似 | B. | ∠A=∠E时,两三角形相似 | ||
| C. | ∠B=∠E时,两三角形相似 | D. | $\frac{AB}{BC}=\frac{DF}{EF}$时,两三角形相似 |
分析 根据等腰三角形的性质和三角形内角和定理,由∠A=∠D时,则∠B=∠C=∠E=∠F,则根据有两组角对应相等的两个三角形相似可对A进行判断;由∠A=∠E得不到第二组角对应相等,则可对B进行判断;根据等腰三角形的性质,由∠B=∠E时,则∠B=∠C=∠E=∠F,则根据有两组角对应相等的两个三角形相似可对C进行判断;根据等腰三角形的性质和三组对应边的比相等的两个三角形相似可对D进行判断.
解答 解:A、∠A=∠D时,则∠B=∠C=∠E=∠F,所以△ABC∽△DEF,所以A选项的判断正确;
B、∠A=∠E时,不能判断△ABC∽△DEF,所以B选项的判断不正确;
C、∠B=∠E时,则∠B=∠C=∠E=∠F,所以△ABC∽△DEF,所以C选项的判断正确;
D、若$\frac{AB}{BC}$=$\frac{DF}{EF}$,则$\frac{AB}{DF}$=$\frac{BC}{EF}$,所以$\frac{AB}{DF}$=$\frac{AC}{DE}$=$\frac{BC}{EF}$,所以D选项的判断正确.
故选B.
点评 本题考查了相似三角形的判定:三组对应边的比相等的两个三角形相似;两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.也考查了等腰三角形的性质.


科目:初中数学 来源: 题型:选择题
| A. | x2-x-2=2 | B. | x2-x-4=0 | C. | x2-x=0 | D. | x2+x-4=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=-x2+2x+2,
已知二次函数y=-x2+2x+2,| x | … | … | |||||
| y | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
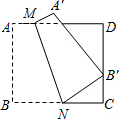 如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的点B′处,点A的对应点为点A′,且B′C=3,则B′N的长是( )
如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的点B′处,点A的对应点为点A′,且B′C=3,则B′N的长是( )| A. | 3 | B. | 4 | C. | 5 | D. | 4.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 用8m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长,宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?
用8m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长,宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com