
 用8m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长,宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?
用8m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长,宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?分析 (1)设窗的高度为xm,宽为($\frac{8-2x}{3}$)m,根据矩形面积公式列出二次函数关系式;
(2)根据长宽均为正数,列不等式组即可解答;
(3)利用二次函数性质求出最值,再考虑取值范围即可.
解答 解:(1)设窗的高度为xm,宽为($\frac{8-2x}{3}$)m,
故S=$\frac{x(8-2x)}{3}$=-$\frac{2}{3}$x2+$\frac{8}{3}$x.
故答案为:S=-$\frac{2}{3}$x2+$\frac{8}{3}$x.
(2)根据题意x满足$\left\{\begin{array}{l}{x>0}\\{\frac{8-2x}{3}>0}\end{array}\right.$,
解得:0<x<4.
故答案为:0<x<4;
(3)∵S=-$\frac{2}{3}$x2+$\frac{8}{3}$x=-$\frac{2}{3}$(x-2)2+$\frac{8}{3}$.
∴当x=2m时,S最大值为$\frac{8}{3}$m2,
∵0<2<4,
∴最大透光面积能在自变量取值范围内取到.
点评 本题主要考查了二次函数的应用,根据矩形面积公式列出函数表达式是解决问题的关键.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:选择题
| A. | ∠A=∠D时,两三角形相似 | B. | ∠A=∠E时,两三角形相似 | ||
| C. | ∠B=∠E时,两三角形相似 | D. | $\frac{AB}{BC}=\frac{DF}{EF}$时,两三角形相似 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
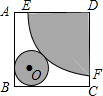 要按图所示的方式,剪裁边长为a正方形铁片,以扇形EDF为侧面、⊙O为底面制作圆锥模型.设DE=R,⊙O的半径为r.
要按图所示的方式,剪裁边长为a正方形铁片,以扇形EDF为侧面、⊙O为底面制作圆锥模型.设DE=R,⊙O的半径为r.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com