
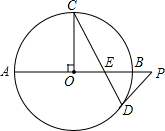
 如图,AB是⊙O的直径,半径OC⊥AB,P是AB延长线上一点,PD切⊙O于点D,CD交AB于点E,判断△PDE的形状,并说明理由.
如图,AB是⊙O的直径,半径OC⊥AB,P是AB延长线上一点,PD切⊙O于点D,CD交AB于点E,判断△PDE的形状,并说明理由.  手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:解答题
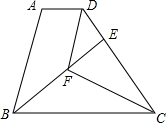 已知,如图,在梯形ABCD中,AD∥BC,BC=CD,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.
已知,如图,在梯形ABCD中,AD∥BC,BC=CD,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=-x2+2x+2,
已知二次函数y=-x2+2x+2,| x | … | … | |||||
| y | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
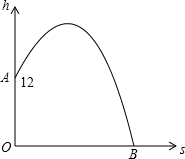 家在四楼的小明从窗口A向楼外掷出一个纸飞机,如果纸飞机下落过程值距离地面的高度h(米)与飞机的水平距离s(米)之间的关系式是h=-$\frac{1}{20}$s2+$\frac{2}{5}$s+m,其图象如图所示,那么这架纸飞机落地处点B与小明家所住的楼的相距20米.
家在四楼的小明从窗口A向楼外掷出一个纸飞机,如果纸飞机下落过程值距离地面的高度h(米)与飞机的水平距离s(米)之间的关系式是h=-$\frac{1}{20}$s2+$\frac{2}{5}$s+m,其图象如图所示,那么这架纸飞机落地处点B与小明家所住的楼的相距20米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 用8m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长,宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?
用8m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长,宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
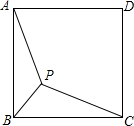 如图,已知点P是正方形ABCD内的一点,连结PA、PB、PC.若PA=4,PB=2,∠APB=135°,则PC的长为2$\sqrt{6}$.
如图,已知点P是正方形ABCD内的一点,连结PA、PB、PC.若PA=4,PB=2,∠APB=135°,则PC的长为2$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com