
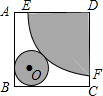
 要按图所示的方式,剪裁边长为a正方形铁片,以扇形EDF为侧面、⊙O为底面制作圆锥模型.设DE=R,⊙O的半径为r.
要按图所示的方式,剪裁边长为a正方形铁片,以扇形EDF为侧面、⊙O为底面制作圆锥模型.设DE=R,⊙O的半径为r.分析 (1)利用底面周长=展开图的弧长求出半径比;
(2)根据题意列方程$\sqrt{2}$r+r=$\sqrt{2}$a-R,$\sqrt{2}$r+r=$\sqrt{2}$a-4r,代入a的值即可得到结果.
解答 解:(1)利用底面周长=展开图的弧长可得;
2πr=$\frac{90πR}{180}$,
解得:R=4r;
(2)根据题意得:$\sqrt{2}$r+r=$\sqrt{2}$a-R,$\sqrt{2}$r+r=$\sqrt{2}$a-4r,
解得:r=$\frac{\sqrt{2}a}{5+\sqrt{2}}$,
当a=5$\sqrt{2}+$2时,r=2.
点评 本题考查了相切两圆的性质,列方程求未知数的值,关键是利用底面周长=展开图的弧长求得r与R的关系.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:选择题
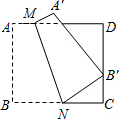 如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的点B′处,点A的对应点为点A′,且B′C=3,则B′N的长是( )
如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的点B′处,点A的对应点为点A′,且B′C=3,则B′N的长是( )| A. | 3 | B. | 4 | C. | 5 | D. | 4.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 用8m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长,宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?
用8m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长,宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
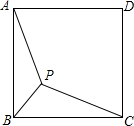 如图,已知点P是正方形ABCD内的一点,连结PA、PB、PC.若PA=4,PB=2,∠APB=135°,则PC的长为2$\sqrt{6}$.
如图,已知点P是正方形ABCD内的一点,连结PA、PB、PC.若PA=4,PB=2,∠APB=135°,则PC的长为2$\sqrt{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com