
 正方形ABCD的边长为a,以相邻的两边为直径分别画两个半圆,求阴影部分的面积.
正方形ABCD的边长为a,以相邻的两边为直径分别画两个半圆,求阴影部分的面积. 分析 先判断出两半圆交点为正方形的中心,连接OB,则可得出所产生的四个小弓形的面积相等,继而根据阴影部分的面积可得出答案.
解答 解:易知:两半圆的交点即为正方形的中心,设此点为O,连接AC,则AC必过点O,连接OB;
则图中的四个小弓形的面积相等,
∴两个半圆的面积-Rt△ABC的面积=4个小弓形的面积,
∴两个小弓形的面积为($\frac{π{a}^{2}}{8}-\frac{{a}^{2}}{4}$),
图中阴影部分的面积=正方形面积-[Rt△ADC-2个小弓形的面积]=a2-[$\frac{1}{2}{a}^{2}$-($\frac{π{a}^{2}}{8}-\frac{{a}^{2}}{4}$)].
点评 此题考查了扇形的面积计算,解答本题的关键是得出两半圆的交点是正方形的中心,求出小弓形的面积,有一定难度,注意仔细观察图形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
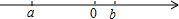 有理数a、b在数轴上如图,
有理数a、b在数轴上如图,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=-x2+2x+3.
已知二次函数y=-x2+2x+3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com