

 的值
的值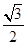
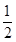 CG(30°角所对直角边等于斜边一半)、BG=
CG(30°角所对直角边等于斜边一半)、BG=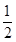 CG,故可得出BG+DG=CG;?结合前面求得结论,设出未知数,根据勾股定理和等腰三角形的性质即可求出比例性质.
CG,故可得出BG+DG=CG;?结合前面求得结论,设出未知数,根据勾股定理和等腰三角形的性质即可求出比例性质. =
=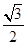 .
.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
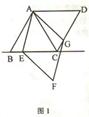
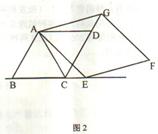
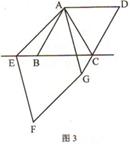
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
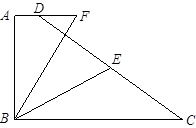
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com