
【题目】如图正方形ABCD中,点E、F分别在CD、BC边上,△AEF是等边三角形.以下结论:①EC=FC;②∠AED=75°;③AF=![]() CE;④EF的垂直平分线是直线AC.正确结论个数有( )个.
CE;④EF的垂直平分线是直线AC.正确结论个数有( )个.

A. 1B. 2C. 3D. 4
【答案】D
【解析】
由题意可证△ABF≌△ADE,可得BF=DE,即可得EC=CF,由勾股定理可得EF=![]() EC,由平角定义可求∠AED=75°,由AE=AF,EC=FC可证AC垂直平分EF,
EC,由平角定义可求∠AED=75°,由AE=AF,EC=FC可证AC垂直平分EF,
则可判断各命题是否正确.
∵四边形ABCD是正方形,
∴AB=AD=BC=CD,∠B=∠C=∠D=∠DAB=90°
∵△AEF是等边三角形
∴AE=AF=EF,∠EAF=∠AEF=60°
∵AD=AB,AF=AE
∴△ABF≌△ADE
∴BF=DE
∴BC-BF=CD-DE
∴CE=CF
故①正确
∵CE=CF,∠C=90°
∴EF=![]() CE,∠CEF=45°
CE,∠CEF=45°
∴AF=![]() CE,
CE,
∵∠AED=180°-∠CEF-∠AEF
∴∠AED=75°
故②③正确
∵AE=AF,CE=CF
∴AC垂直平分EF
故④正确
故选:D.


科目:初中数学 来源: 题型:
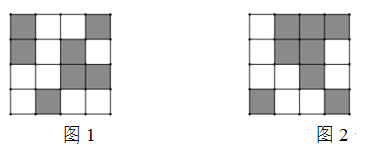
【题目】某校利用二维码进行学生学号统一编排.黑色小正方形表示1,白色小正方形表示0,将每一行数字从左到右依次记为a,b,c,d,那么利用公式a×23-b×22-c×21+d计算出每一行的数据.第一行表示年级,第二行表示班级,如图1所示,第一行数字从左往右依次是1,0,0,1,则表示的数据为1×23+0×22+0×21+1=9,计作09,第二行数字从左往右依次是1,0,1,0,则表示的数据为1×23+0×22+1×21=10,计作10,以此类推,图1代表的统一学号为091034,表示9年级10班34号.小明所对应的二维码如图2所示,则他的编号是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里装有3个黑球和若干白球,它们除颜色外都相同.在不允许将球倒出来数的前提下,小明为估计其中白球数,采用如下办法:随机从中摸出一球,记下颜色后放回袋中,充分摇匀后,再随机摸出一球,记下颜色,…不断重复上述过程.小明共摸100次,其中20次摸到黑球.根据上述数据,小明估计口袋中白球大约有( )
A. 10个 B. 12 个 C. 15 个 D. 18个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级所有女生的身高统计数据如下表,请回答下列问题:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) 这个学校八年级共有多少女生?
(2) 身高在 ![]() 到
到 ![]() 的女生有多少人?
的女生有多少人?
(3) 一女生的身高恰好为 ![]() ,哪一组包含这个身高?这一组出现的频数、频率各是多少?
,哪一组包含这个身高?这一组出现的频数、频率各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班同学为了解 2011 年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.请解答以下问题:

![]()

(1) 把上面的频数分布表和频数分布直方图补充完整;
(2) 求月均用水量不超过 ![]() 的家庭数占被调查家庭总数的百分比;
的家庭数占被调查家庭总数的百分比;
(3) 若该小区有 ![]() 户家庭,根据调查数据估计,该小区月均用水量超过
户家庭,根据调查数据估计,该小区月均用水量超过 ![]() 的家庭大约有多少户 ?
的家庭大约有多少户 ?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙0经过点D,E是⊙O上一点,且∠AED=45°,

(1)求证:CD是⊙O的切线.
(2)若⊙O的半径为3,AE=5,求∠DAE的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在平面直角坐标系中直线y=x﹣2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).
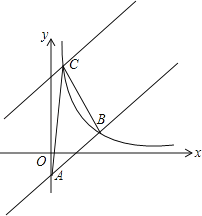
(1)求反比例函数的关系式;
(2)将直线y=x﹣2向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是1个直角三角形和2个小正方形,直角三角形的三条边长分别是a,b,c,其中a,b是直角边,正方形的边长分别是a、b.
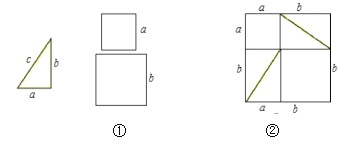
(1)将4个完全一样的直角三角形和2个小正方形构成一个大正方形(如图②).用两种不同的方法列代数式表示图②中的大正方形面积:
方法一:______________________________;
方法二:______________________________;
(2)观察图②,试写出![]() ,
,![]() ,
,![]() ,
,![]() 这四个代数式之间的等量关系;
这四个代数式之间的等量关系;
(3)利用(2)的结论计算![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com