
【题目】某中学为落实市教育局提出的“全员育人,创办特色学校”的会议精神,决心打造“书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.符合题意的组建方案有( )种.
A. 1种 B. 2种 C. 3种 D. 4种
【答案】C
【解析】
设组建中型两类图书角x个、小型两类图书角(30-x)个,由于组建中、小型两类图书角共30个,已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.若组建一个中型图书角的费用是860本,组建一个小型图书角的费用是570本,因此可以列出不等式组![]() , 解不等式组然后去整数即可求解.
, 解不等式组然后去整数即可求解.
解:设组建中型图书角x个,则组建小型图书角为(30-x)个.
由题意,得![]()
化简得,![]()
解这个不等式组,得18≤x≤20.
∵由于x只能取整数,
∴x的取值是18,19,20.
当x=18时,30-x=12;当x=19时,30-x=11;当x=20时,30-x=10.
故有三种组建方案:
方案一,中型图书角18个,小型图书角12个;
方案二,中型图书角19个,小型图书角11个;
方案三,中型图书角20个,小型图书角10个.
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(9分)已知代数式(ax-3)(2x+4)-x2-b化简后,不含x2项和常数项.
(1)求a,b的值;
(2)求(2a+b)2-(a-2b)(a+2b)-3a(a-b)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制成下面两幅不完整的统计图,请你根据图中提供的信息解答下列问题:

(1)在这次调查中,一共调查了 名学生;
(2)补全条形统计图;
(3)若该校共有1500名学生,估计爱好运动的学生有 人;
(4)在全校同学中随机选取一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OA平分∠EOC.

(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,三角形的三条中线一定会交于一点,这一点就叫做三角形的重心.重心有很多美妙的性质,如关于线段比.面积比就有一些“漂亮”结论,利用这些性质可以解决三角形中的若干问题.请你利用重心的概念完成如下问题: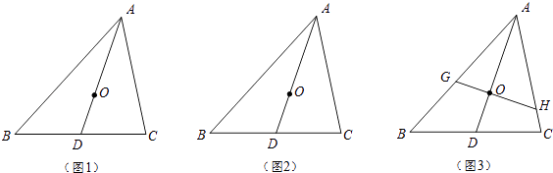
(1)若O是△ABC的重心(如图1),连结AO并延长交BC于D,证明: ![]() ;
;
(2)若AD是△ABC的一条中线(如图2),O是AD上一点,且满足 ![]() ,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;
,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;
(3)若O是△ABC的重心,过O的一条直线分别与AB、AC相交于G、H(均不与△ABC的顶点重合)(如图3),S四边形BCHG , S△AGH分别表示四边形BCHG和△AGH的面积,试探究 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC 的角平分线与 BC 的垂直平分线交于点 D,DE⊥AB, DF⊥AC,垂足分别为 E,F.若 AB=10,AC=8,求 BE 长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径r=25,四边形ABCD内接于圆⊙O,AC⊥BD于点H,P为CA延长线上的一点,且∠PDA=∠ABD. 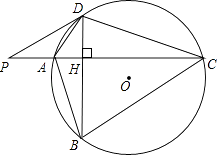
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若tan∠ADB= ![]() ,PA=
,PA= ![]() AH,求BD的长;
AH,求BD的长;
(3)在(2)的条件下,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选取最关注的一个),根据调查结果绘制了两幅不完整的统计图,根据图中提供的信息,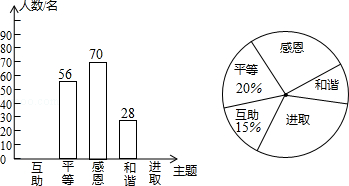
解答下列问题:
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整;并写出这次主题班会调查结果的众数是;中位数落在的区域是 .
(3)若该校学生人数为800人,请根据上述调查结果,估计该校学生中“感恩”的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com