
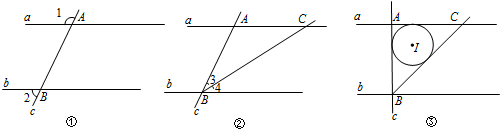
分析 (1)根据平行线的性质和邻补角的定义即可得到结论;
(2)根据平行线的性质得到∠ACB=∠4,等量代换得到∠ACB=∠3,由等腰三角形的判定即可得到结论;
(3)①由(2)得AB=AC,推出△ABC是等腰直角三角形.根据勾股定理得到BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=2$\sqrt{2}$,由⊙I为△ABC的内切圆,得到四边形ADIF是正方形.根据切线长定理得到r=AD=$\frac{AB+AC-BC}{2}$=2-$\sqrt{2}$,于是得到结论;
②当点P在射线AC上时,得到0≤AP≤2$\sqrt{3}$-$\sqrt{6}$+2-$\sqrt{2}$,当点P在射线AC的反向延长线上时,得到0≤AP≤2$\sqrt{3}$-$\sqrt{6}$-2+$\sqrt{2}$.
解答 解:(1)∠1+∠2=180°,
故答案为:∠1+∠2=180°;
(2)当∠3=∠4时,AB=AC,
证明:∵a∥b,
∴∠ACB=∠4,
又∵∠3=∠4,
∴∠ACB=∠3,
∴AB=AC;
(3)①由(2)得AB=AC,
又∵∠BAC=90°,
∴△ABC是等腰直角三角形.
∵AB=2,
∴AC=2.
∴在Rt△ABC中,BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=2$\sqrt{2}$.
设D、E、F分别为边AB、BC、AC上的切点,
连接ID、IE、IF,
∵⊙I为△ABC的内切圆,
∴ID⊥AB、IE⊥BC、IF⊥AC.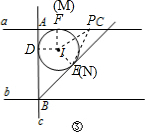
∴AD=AF,BD=BE,CE=CF.
∵∠BAC=90°,
∴四边形ADIF是矩形.
∵ID=IF,
∴矩形ADIF是正方形.
∴r=AD=$\frac{AB+AC-BC}{2}$=2-$\sqrt{2}$.
∴⊙I的半径为2-$\sqrt{2}$;
②如图,当点P在射线AC上时,点M与F重合,N与E重合,∠MPN=60°,∴∠PNI=∠PIE=75°,∴∠FIP=60°,
∴PF=$\sqrt{3}$FI=2$\sqrt{3}$-$\sqrt{6}$,∴PA=3$\sqrt{3}$-$\sqrt{6}$,∴0≤AP≤2$\sqrt{3}$-$\sqrt{6}$+2-$\sqrt{2}$,
同理,当点P在射线AC的反向延长线上时,0≤AP≤2$\sqrt{3}$-$\sqrt{6}$-2+$\sqrt{2}$.
点评 本题考查了切线的判定和性质,平行线的判定和性质,勾股定理,正方形的判定和性质,内切圆的性质,等腰三角形的判定,等腰直角三角形的性质,证得矩形ADIF是正方形,是解决(3)小题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 9186×103 | B. | 9.186×105 | C. | 9.186×106 | D. | 9.186×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
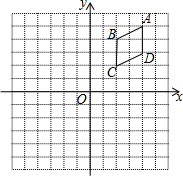 如图,在平面直角坐标系中,四边形ABCD的四个顶点坐标分别为A(4,5)、B(2,4)、C(2,2)、D(4,3).(每个方格的边长均为1个单位长度)
如图,在平面直角坐标系中,四边形ABCD的四个顶点坐标分别为A(4,5)、B(2,4)、C(2,2)、D(4,3).(每个方格的边长均为1个单位长度)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
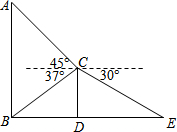 某班数学兴趣小组为了测量建筑物AB的高度,他们选取了地面上一点E,测得DE的长度为8.65米,并以建筑物CD的顶端点C为观测点,测得点A的仰角为45°,点B的俯角为37°,点E的俯角为30°.
某班数学兴趣小组为了测量建筑物AB的高度,他们选取了地面上一点E,测得DE的长度为8.65米,并以建筑物CD的顶端点C为观测点,测得点A的仰角为45°,点B的俯角为37°,点E的俯角为30°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com