
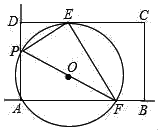
【题目】如图,矩形ABCD中,AD=10,CD=15,E是边CD上一点,且DE=5,P是射线AD上一动点,过A,P,E三点的⊙O交直线AB于点F,连结PE,EF,PF,设AP=m.
(1)当m=6时,求AF的长.
(2)在点P的整个运动过程中.
①tan∠PFE的值是否改变?若不变,求出它的值;若改变,求出它的变化范围.
②当矩形ABCD恰好有2个顶点落在⊙O上时,求m的值.
(3)若点A,H关于点O成中心对称,连结EH,CH.当△CEH是等腰三角形时,求出所有符合条件的m的值.(直接写出答案即可)
【答案】(1)13;(2)① tan∠PFE的值不变, tan∠PFE=![]() ;②m=5;(3) 满足条件的m的值为10﹣5
;②m=5;(3) 满足条件的m的值为10﹣5![]() 或10﹣2
或10﹣2![]() 或
或![]() 或10+3
或10+3![]()
【解析】
(1)做辅助线,根据勾股定理,相似成比例求值.(2)根据几何关系和应用公式进而得出tan∠PFE的值不变,再根据题干的特殊条件求出m.(3)根据几何关系多次利用勾股定理求解.
(1)如图1中,连接AE.
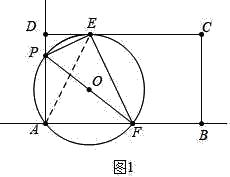
在Rt△DPE中,∵DE=5,DP=AD﹣AP=4,
∴PE=![]() =
=![]() ,
,
在Rt△ADE中,AE=![]() =5
=5![]() ,
,
∵∠PAF=90°,
∴PF是⊙O的直径,
∴∠PEF=∠ADF=90°,
∵∠DAE=∠PFE,
∴△ADE∽△FEP,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴PF=![]() ,
,
在Rt△PAF中,AF=![]() =
=![]() =13.
=13.
(2)①tan∠PFE的值不变.
理由:如图1中,∵∠PFE=∠DAE,
∴tan∠PFE=tan∠DAF=![]() =
=![]() .
.
②如图2中,当⊙O经过A、D时,点P与D重合,此时m=10.
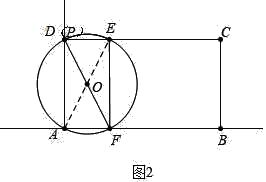
如图3中,当⊙O经过A、B时,
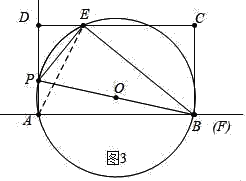
在Rt△BCE中,BE=![]() =10
=10![]() ,
,
∵tan∠PFE=![]() ,
,
∴PE=5![]() ,
,
∴PD=![]() =5,
=5,
∴m=PA=5.
如图4中当⊙O经过AC时,作FM⊥DC交DC的延长线于M.
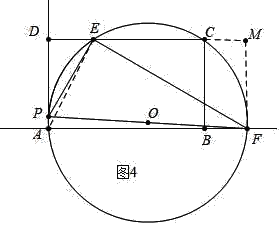
根据对称性可知,DE=CM=BF=5,
在Rt△EFM中,EF=![]() =5
=5![]() ,
,
∴PE=![]() EF=
EF=![]() ,
,
∴PD=![]() =
=![]() ,
,
∴m=AD﹣PD=![]() ,
,
综上所述,m=10或5或![]() 时,矩形ABCD恰好有2个顶点落在⊙O上
时,矩形ABCD恰好有2个顶点落在⊙O上
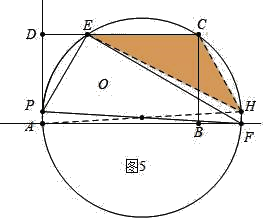
(3)如图5中,当EC=CH时,根据对称性可知:PE=CH=EC=10,PD=![]() =5
=5![]() ,
,
∴m=10﹣5![]() .
.
如图6中当EC=EH=10时,
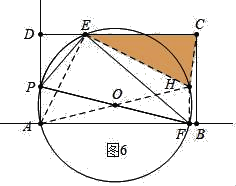
在Rt△AEH中,AH=![]() =
=![]() =5
=5![]() ,
,
易知PF=AH=5![]() ,
,
∵∴∴PE:EF:PF=1:2:![]() ,
,
∴PE=![]() ,
,
在Rt△PDE中,DP=![]() =2
=2![]() ,
,
∴m=PA=AD﹣PD=10﹣2![]() .
.
如图7中当HC=HE时,延长FH交CD于M,则EM=CM=BF=5,HM=![]() ,
,
∴m=PA=HF=10﹣![]() =
=![]() .
.
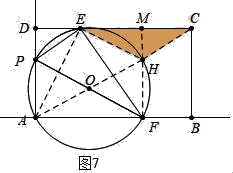
如图8中,当EH=EC时,
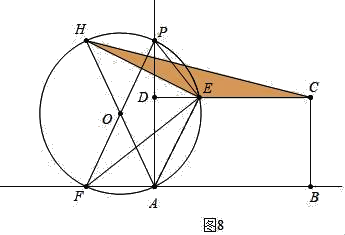
PF=AH=![]() =
=![]() =5
=5![]() ,
,
∵PE:EF:PF=1:2:![]() ,
,
∴PE=![]() ,
,
在Rt△PDE中,PD=![]() =3
=3![]() ,
,
∴m=PA=AD+PD=10+3![]() ,
,
综上所述,满足条件的m的值为10﹣5![]() 或10﹣2
或10﹣2![]() 或
或![]() 或10+3
或10+3![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(1)操作发现:
在△ABC中,AB=AC,∠BAC=90°,D在线段BC上(不与点B重合),连接AD,将线段AD绕A点逆时针旋转90°得到AE,连接EC,如图①所示,请直接写出线段CE和BD的位置关系和数量关系.
(2)猜想论证:
在(1)的条件下,当D在线段BC的延长线上时,请你在图②中画出图形并判断(1)中的结论是否成立,并证明你的判断.
(3)拓展延伸:
如图③,若AB≠AC,∠BAC≠90°,点D在线段BC上运动,试探究:当锐角∠ACB等于 度时,线段CE和BD之间的位置关系仍成立(点C、E重合除外)?此时若作DF⊥AD交线段CE于点F,且当AC=3![]() 时,请直接写出线段CF的长的最大值是 .
时,请直接写出线段CF的长的最大值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在y轴上,其坐标为(0,4),x轴上的一动
P从原点O出发,沿x轴正半轴方向运动,速度为每秒1个单位长度,以P为直角顶点
第一象限内作等腰Rt△APB.设P点的运动时间为t秒.

(1)填空:当t=2时,点B的坐标为.
(2)在P点的运动过程中,当AB∥x轴时,求t的值;
(3)通过探索,发现无论P点运动到何处,点B始终在一直线上,试求出该直线的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,将AB边沿AD折叠,发现B点的对应点E正好在AC的垂直平分线上,则∠C=_______
查看答案和解析>>
科目:初中数学 来源: 题型:
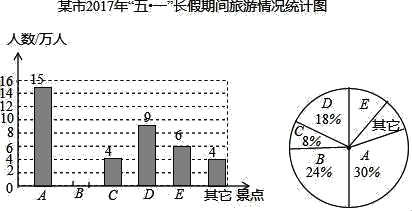
【题目】随着道路交通的不断完善,某市旅游业快速发展,该市旅游景区有A、B、C、D、E等著名景点,市旅游部门统计绘制出2017年“五一”长假期间旅游情况统计图(不完整)如下所示,根据相关信息解答下列问题:
(1)2017年“五一”期间,该市旅游景点共接待游客 万人,扇形统计图中A景点所对应的圆心角的度数是 ,并补全条形统计图.
(2)在等可能性的情况下,甲、乙两个旅行团在A、B、D三个景点中选择去同一景点的概率是多少?请用画树状图或列表加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图 1 所示放置,图 2 是由它抽像出的几何图形,B, C, E在同一 条直线上,连结DC.

(1)请找出图 2 中的全等三角形,并给予证明(说明:结论中不得含有未标识的字 母);
(2)证明:DC ⊥ BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
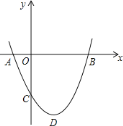
【题目】如图,二次函数![]() .图象的顶点为
.图象的顶点为![]() ,其图象与
,其图象与![]() 轴的交点
轴的交点![]() 、
、![]() 的横坐标分别为
的横坐标分别为![]() 、
、![]() ,与
,与![]() 轴负半轴交于点
轴负半轴交于点![]() .下面五个结论:①
.下面五个结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 随
随![]() 值的增大而增大;④当
值的增大而增大;④当![]() 时,
时,![]() ;⑤只有当
;⑤只有当![]() 时,
时,![]() 是等腰直角三角形.那么,其中正确的结论______.(只填你认为正确结论的序号)
是等腰直角三角形.那么,其中正确的结论______.(只填你认为正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年南宁市地铁
年南宁市地铁![]() 号线二期工程建设如火如荼.预计
号线二期工程建设如火如荼.预计![]() 年底投入运营,从此省城南宁市将进入立体大交通新时代.甲、乙两个工程队计划参与其中的一项工程建设,甲队单独施工
年底投入运营,从此省城南宁市将进入立体大交通新时代.甲、乙两个工程队计划参与其中的一项工程建设,甲队单独施工![]() 天完成该项工程的
天完成该项工程的![]() ,这时乙队加入,两队还需同时施工
,这时乙队加入,两队还需同时施工![]() 天才能完成该项工程.
天才能完成该项工程.
![]() 若乙队单独施工,需要多少天才能完成该项工程?
若乙队单独施工,需要多少天才能完成该项工程?
![]() 若甲队参与该项工程施工的时间不超过
若甲队参与该项工程施工的时间不超过![]() 天,则乙队至少施工多少天才能完成该项工程?
天,则乙队至少施工多少天才能完成该项工程?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com