
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��y���ϣ�������Ϊ��0��4����x���ϵ�һ��
P��ԭ��O��������x�������᷽���˶����ٶ�Ϊÿ��1����λ���ȣ���PΪֱ�Ƕ���
��һ������������Rt��APB����P����˶�ʱ��Ϊt�룮

��1����գ���t��2ʱ����B������Ϊ��
��2����P����˶������У���AB��x��ʱ����t��ֵ��
��3��ͨ��̽������������P���˶����δ�����Bʼ����һֱ���ϣ��������ֱ�ߵĺ�������ʽ��
���𰸡���1������2��4������2��t=4����3��y��x��4
��������
��1������P����������ƽ��2����λ�����O����ʱ����A������Ϊ������2��4��������AΧ�Ƶ�O˳ʱ����ת90������ʱ��B������Ϊ����4��2��������B����������ƽ��2����λ����Ϊ��ʱ�ĵ�B��6��2����������⣻
��2������B��BC��x���ڵ�C����ͼ��ʾ��֤���ı���ABCOΪ�����Σ���AO��BC��4�����APBΪ����ֱ�������Σ�������⣻
��3��֤����PAO�ա�BPC��AAS������AP��BP��AO��PC��BC��PO����A��0��4������P��t��0������B��x��y������PC��AO��4��BC��PO��t��y��CO��PC+PO��4+y��x��������⣮
��1������P����������ƽ��2����λ�����O����ʱ����A������Ϊ������2��4����
����AΧ�Ƶ�O˳ʱ����ת90������ʱ��B������Ϊ����4��2����
����B����������ƽ��2����λ����Ϊ��ʱ�ĵ�B��6��2����
��2������B��BC��x���ڵ�C����ͼ��ʾ��

��AO��x�ᣬBC��x�ᣬ��AB��x�ᣬ
���ı���ABCOΪ�����Σ�
��AO��BC��4��
�ߡ�APBΪ����ֱ�������Σ�
��AP��BP����PAB����PBA��45����
���OAP��90������PAB��45����
���AOPΪ����ֱ�������Σ�
��OA��OP��4��t��4��1��4���룩��
��3���ߡ�APBΪ����ֱ�������Σ�
���APO+��BPC��180����90����90����
�֡ߡ�PAO+��APO��90�������PAO����BPC��
��PAO����BPC��
�ڡ�PAO�͡�BPC�У���AOP����PCB��90����
���PAO�ա�BPC��AAS����
AP��BP��
��AO��PC��BC��PO��
�ߵ�A��0��4������P��t��0������B��x��y����
��PC��AO��4��BC��PO��t��y��CO��PC+PO��4+y��x��
��y��x��4��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����Rt��ABC�У���BAC��90������D�ӵ�B�������߶�BC�ƶ�����ADΪ��������Rt��ADE����DAE��90��������CE��
����ͼ����֤����ACE�ա�ABD��
����֤��BD2��CD2��2AD2��
����AB��4�����ʣ���DCE�������û�����ֵ����û����˵�����ɣ�������������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С���İְ��ڳر߿���һ���ı����������߲ˣ��ְ���С������һ�����ص�������Ա�������.С�������׳ߺͲ���ǣ����AB=3�ף�BC=4�ף�CD=12�ף�DA=13�ף���B=90��.
��������AC����֤������ACD��ֱ�������Σ�
�������С������������ص����Ϊ___________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABΪб�ߵ�Rt��ABC��ÿ����Ϊ�������������Σ��ֱ���������ABMN��������BCPQ��������ACEF���ұ�EFǡ�þ�����N����S3��S4��6����S1+S5��_____����ע��ͼ����ʾ���S��ʾ��Ӧ���������������S3��ʾ��ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijʵ����ѧΪ�˽�ѧ�������ʺ��Լ��Ŀ�ǰ��ѹ��ʽ�����ھ��꼶��Χ�ڿ�չ��һ�γ������飬ѧ������������ѡ����ѡ��һ�С�����ݵ����������������в�������ͳ��ͼ��
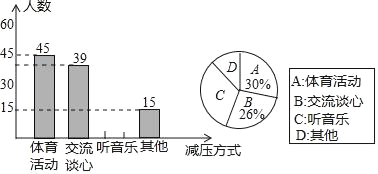
�����������Ϣ����������⣺
��1����γ��������У�����ѧ������Ϊ______�ˣ�
��2���벹ȫ����ͳ��ͼ��
��3������ͳ��ͼ��������������Ӧ����Բ�Ľ�Ϊ______�ȣ�
��4����ʵ����ѧ���꼶��700�ˣ�����Ʋ���������������Ϊ��ѹ��ʽ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ɽ���������мס��������ǹ�����kg�������ǹ����ۼۺͽ������
�ǹ� | ���� | ���� |
�ۼ� | 36Ԫ/kg | 20Ԫ/kg |
���� | 30Ԫ/kg | 16Ԫ/kg |
��1���������üס��������ǹ���ϳ��Ӱ��dz��ۣ���Ϻ��ǹ����ۼ���27.2Ԫ/kg����Ҫ���������Ӱ��ǹ�100/kg����Ҫ�ס��������ǹ�������ǧ�ˣ�
��2������һ����ͯ��ǰϦ����������5000Ԫ�����ס��������ǹ���200kg����ν�������ʹ�����ǹ�������������������Ƕ��٣���ע��������ֻ��Ϊ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��x2+bx+c��x���ཻ��A��B���㣬��y���ཻ�ڵ�C���ҵ�B���C������ֱ�ΪB��3��0����C��0��3������M�������ߵĶ��㣮
��1������κ����Ĺ�ϵʽ��
��2����PΪ�߶�MB��һ�����㣬����P��PD��x���ڵ�D����OD=m����PCD�����ΪS�����ж�S�����ֵ����Сֵ����˵�����ɣ�
��3����MB���Ƿ���ڵ�P��ʹ��PCDΪֱ�������Σ�������ڣ��������P�����ꣻ��������ڣ���˵�����ɣ�
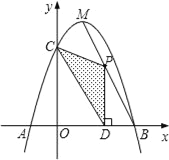
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AD=10��CD=15��E�DZ�CD��һ�㣬��DE=5��P������AD��һ���㣬��A��P��E����ġ�O��ֱ��AB�ڵ�F������PE��EF��PF����AP=m��
��1����m=6ʱ����AF�ij���
��2���ڵ�P�������˶������У�
��tan��PFE��ֵ�Ƿ�ı䣿�����䣬�������ֵ�����ı䣬������ı仯��Χ��
�ڵ�����ABCDǡ����2���������ڡ�O��ʱ����m��ֵ��
��3������A��H���ڵ�O�����ĶԳƣ�����EH��CH������CEH�ǵ���������ʱ��������з���������m��ֵ����ֱ��д���𰸼��ɣ�
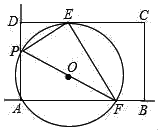
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ģ���ͼ����֪������ABCD����E��BC�ߵ��е㣬DE��AC�ཻ�ڵ�F������BF�����н��ۣ���S��ABF=S��ADF����S��CDF=2S��CEF����S��ADF=2S��CEF����S��ADF=2S��CDF��������ȷ���ǣ�������

A. �٢ڢ� B. �ڢ� C. �٢� D. �٢ڢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com