
【题目】(题文)如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF;②S△CDF=2S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF,其中正确的是( )

A. ①②③ B. ②③ C. ①④ D. ①②④
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在y轴上,其坐标为(0,4),x轴上的一动
P从原点O出发,沿x轴正半轴方向运动,速度为每秒1个单位长度,以P为直角顶点
第一象限内作等腰Rt△APB.设P点的运动时间为t秒.

(1)填空:当t=2时,点B的坐标为.
(2)在P点的运动过程中,当AB∥x轴时,求t的值;
(3)通过探索,发现无论P点运动到何处,点B始终在一直线上,试求出该直线的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
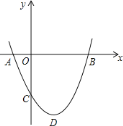
【题目】如图,二次函数![]() .图象的顶点为
.图象的顶点为![]() ,其图象与
,其图象与![]() 轴的交点
轴的交点![]() 、
、![]() 的横坐标分别为
的横坐标分别为![]() 、
、![]() ,与
,与![]() 轴负半轴交于点
轴负半轴交于点![]() .下面五个结论:①
.下面五个结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 随
随![]() 值的增大而增大;④当
值的增大而增大;④当![]() 时,
时,![]() ;⑤只有当
;⑤只有当![]() 时,
时,![]() 是等腰直角三角形.那么,其中正确的结论______.(只填你认为正确结论的序号)
是等腰直角三角形.那么,其中正确的结论______.(只填你认为正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是⊙O的内接四边形,AC是⊙O的直径,DE⊥AB,垂足为E.
(1)延长DE交⊙O于点F,延长DC,FB交于点P,如图1.求证:PC=PB;
(2)过点B作BG⊥AD,垂足为G,BG交DE于点H,且点O和点A都在DE的左侧,如图2.若AB=![]() ,DH=1,∠OHD=80°,求∠BDE的大小.
,DH=1,∠OHD=80°,求∠BDE的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于任何数a,符号[a]表示不大于a的最大整数.
例如:[5.7]=5,[5]=5,[﹣1.5]=﹣2.
(1)[﹣![]() ]= ;
]= ;
(2)如果[a]=3,那么a的取值范围是 ;
(3)如果[![]() ]=﹣3,求满足条件的所有整数x.
]=﹣3,求满足条件的所有整数x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(0,-1).
(1)画出△ABC关于原点O成中心对称的图形△A1B1C1;
(2)在(1)的条件下直接写出点A1的坐标为______;B1的坐标为______;
(3)求出△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年南宁市地铁
年南宁市地铁![]() 号线二期工程建设如火如荼.预计
号线二期工程建设如火如荼.预计![]() 年底投入运营,从此省城南宁市将进入立体大交通新时代.甲、乙两个工程队计划参与其中的一项工程建设,甲队单独施工
年底投入运营,从此省城南宁市将进入立体大交通新时代.甲、乙两个工程队计划参与其中的一项工程建设,甲队单独施工![]() 天完成该项工程的
天完成该项工程的![]() ,这时乙队加入,两队还需同时施工
,这时乙队加入,两队还需同时施工![]() 天才能完成该项工程.
天才能完成该项工程.
![]() 若乙队单独施工,需要多少天才能完成该项工程?
若乙队单独施工,需要多少天才能完成该项工程?
![]() 若甲队参与该项工程施工的时间不超过
若甲队参与该项工程施工的时间不超过![]() 天,则乙队至少施工多少天才能完成该项工程?
天,则乙队至少施工多少天才能完成该项工程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速![]() 千米/时,已知交警测速点
千米/时,已知交警测速点![]() 到该公路
到该公路![]() 点的距离为
点的距离为![]() 米,
米,![]() ,
,![]() (如图所示),现有一辆汽车由
(如图所示),现有一辆汽车由![]() 往
往![]() 方向匀速行驶,测得此车从
方向匀速行驶,测得此车从![]() 点行驶到
点行驶到![]() 点所用的时间为
点所用的时间为![]() 秒.
秒.
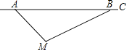
![]() 求测速点
求测速点![]() 到该公路的距离;
到该公路的距离;
![]() 通过计算判断此车是否超速.(参考数据:
通过计算判断此车是否超速.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com