【题目】如图，二次函数
．图象的顶点为
，其图象与
轴的交点
、
的横坐标分别为
、
，与
轴负半轴交于点
．下面五个结论：①
；②
；③当
时，随值的增大而增大；④当
时，
；⑤只有当
时，
是等腰直角三角形．那么，其中正确的结论______．（只填你认为正确结论的序号）
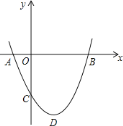
【答案】①⑤
【解析】
根据抛物线的对称性可得到抛物线的对称轴为直线x=1，根据抛物线的对称轴为直线x=﹣
=1可判断①正确；根据图象得x=1对应的函数值为负数，可判断以②错误；
根据抛物线当a＞0，在对称轴左侧，y随x的增大而减小可判断以③错误；利用x=﹣1或x=3时，ax2+bx+c=0，可判断④错误；设抛物线的解析式为y=a（x+1）（x﹣3）=ax2﹣2ax﹣3a，对称轴x=1交x轴与E点，当△ABD是等腰直角三角形，得到DE=
AB，解方程求出a的值即可判断⑤正确．
∵二次函数的图象与x轴的交点A、B的横坐标分别为﹣1、3，∴AB中点坐标为（1，0），而点A与点B是抛物线上的对称点，∴抛物线的对称轴为直线x=1，∴x=﹣=1，即2a+b=0，所以①正确；
∵当x=1时，对应的函数图象在x轴下方，∴a+b+c＜0，所以②错误；
∵a＞0，∴当x≤1时，y随x值的增大而减，所以③错误；
由于当﹣1＜x＜3时，ax2+bx+c＜0，而x=﹣1或x=3时，ax2+bx+c=0，所以④错误；
设抛物线的解析式为y=a（x+1）（x﹣3）=ax2﹣2ax﹣3a，对称轴x=1交x轴与E点，如图，当△ABD是等腰直角三角形，则DE=AB，即|
|=×4，∴a=，所以⑤正确．
故答案为：①⑤．
科目：初中数学 来源： 题型：
【题目】如图，小明的爸爸在池边开了一块四边形土地种蔬菜，爸爸让小明计算一下土地的面积，以便计算产量.小明找了米尺和测角仪，测得AB=3米，BC=4米，CD=12米，DA=13米，∠B=90°.
⑴若连接AC，试证明：△ACD是直角三角形；
⑵请你帮小明计算这块土地的面积为___________.
查看答案和解析>>
科目：初中数学 来源： 题型：
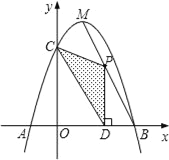
【题目】如图，抛物线y=﹣x2+bx+c与x轴相交于A、B两点，与y轴相交于点C，且点B与点C的坐标分别为B（3，0）．C（0，3），点M是抛物线的顶点．
（1）求二次函数的关系式；
（2）点P为线段MB上一个动点，过点P作PD⊥x轴于点D．若OD=m，△PCD的面积为S，试判断S有最大值或最小值？并说明理由；
（3）在MB上是否存在点P，使△PCD为直角三角形？如果存在，请求出点P的坐标；如果不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
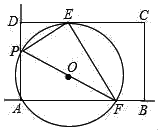
【题目】如图，矩形ABCD中，AD=10，CD=15，E是边CD上一点，且DE=5，P是射线AD上一动点，过A，P，E三点的⊙O交直线AB于点F，连结PE，EF，PF，设AP=m．
（1）当m=6时，求AF的长．
（2）在点P的整个运动过程中．
①tan∠PFE的值是否改变？若不变，求出它的值；若改变，求出它的变化范围．
②当矩形ABCD恰好有2个顶点落在⊙O上时，求m的值．
（3）若点A，H关于点O成中心对称，连结EH，CH．当△CEH是等腰三角形时，求出所有符合条件的m的值．（直接写出答案即可）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】 (1)阅读理解:
我们知道，只用直尺和圆规不能解决的三个经典的希腊问题之一是三等分任意角，但是这个任务可以借助如图所示的一边上有刻度的勾尺完成，勾尺的直角顶点为P，“宽臂”的宽度=PQ= QR = RS,(这个条件很重要哦！)勾 尺的一边 MN 满足M, N, Q三点共线(所以PQ ⊥ MN).
下面以三等分∠ABC为例说明利用勾尺三等分锐角的过程:
第一步:画直线DE使DE //BC，且这两条平行线的距离等于PQ;
第二步:移动勾尺到合适位置，使其顶点P落在DE上，使勾尺的MN边经过点B，同时让点R落在∠ABC的BA边上;
第三步:标记此时点Q和点P所在位置，作射线BQ和射线BP:
请完成第三步操作，图中∠ABC的三等分线是射线 、 .
（2）在(1)的条件下补全三等分∠ABC的主要证明过程:
∵ ，BQ ⊥ PR，
∴BP= BR.（线段垂直平分线上的点与这条线段两个端点的距离相等）
∴∠RBQ=∠PBQ，
∵PT⊥BC，PQ⊥BQ，PT=PQ，
∴∠ = ∠ . （角的内部到角的两边距离相等的点在角的平分线上）
∴∠ = = ∠ = ∠
（3）在（1）的条件下探究：
∠ABS=
∠ABC是否成立？如果成立，请说明理由；如果不成立，请在下图中∠ABC外部画出∠ABV =∠ABC（无需写画法，保留画图痕迹即可）
查看答案和解析>>
科目：初中数学 来源： 题型：
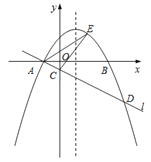
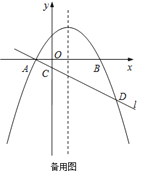
【题目】如图，在平面直角坐标系
中，抛物线
与
轴交于
，
两点（点在点的左侧），经过点的直线
与
轴交于点
，与抛物线的另一个交点为
，且
．
直接写出点的坐标，并求直线
的函数表达式（其中
，
用含
的式子表示）；
点
是直线上方的抛物线上的一点，若
的面积的最大值为
，求的值；
设
是抛物线对称轴上的一点，点
在抛物线上，以点，，，为顶点的四边形能否成为矩形？若能，求出点的坐标；若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在日常生活中，如取款、上网等都需要密码，有一种利用“因式分解”产生的密码，方便记忆，原理是：如多项式
，若
，
时，则各因式的值为
，
，
，于是把018162作为一个六位数的密码，对于多项式
，取
，
时，用上述方法产生的密码是_________________.（写一个即可）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（题文）如图，已知正方形ABCD，点E是BC边的中点，DE与AC相交于点F，连接BF，下列结论：①S△ABF=S△ADF；②S△CDF=2S△CEF；③S△ADF=2S△CEF；④S△ADF=2S△CDF，其中正确的是（ ）
A. ①②③ B. ②③ C. ①④ D. ①②④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，平面直角坐标系中，△ABC的三个顶点坐标分别为A（-2，4）， B（-3，-2），C（1，2）．
（1）画出△ABC关于x轴对称的△A1B1C1，写出点A1、B1、C1的坐标．
（2）在y轴上找一个点P，使△ABP的周长最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com