
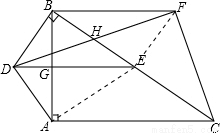
如图,在RtΔABC中,∠BAC=90°,DB⊥BC,DA=DB,点E是BC的中点,DE与AB相交于点G.
(1)求证DE⊥AB;
(2)如果∠FCB=∠FBC=∠DAB,设DF与BC交于点H,求证:DH=FH.

(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)欲证明DE⊥AB,只需推知AE=BE即可;
(2)欲证明DH=FH,需要证得四边形BDEF是平行四边形.
(1)如图,连接AE.
∵∠BAC=90°,BE=EC,
∴AE=BE=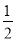 BC.
BC.
又∵DA=DB,
∴DE垂直平分AB,即DE⊥AB;
(2)∵∠DBC=90°
∴∠DBA+∠ABC=90°
∵DA=AB,∴∠DBA=∠DAB,
∵∠FBC=∠DAB
∴∠FBC+∠ABC=90°
∵∠AGE=90°
∴BF∥DE.
又∵∠FBC=∠FCB,
∴FB=FC
∵BE=EC,∴FE⊥BC
∴∠DBE=∠BEF=90°
∴DB∥EF,
∴四边形DBFE是平行四边形,
∴DH=FH.
考点:1.平行四边形的判定与性质;2.线段垂直平分线的性质;3.直角三角形斜边上的中线.


科目:初中数学 来源:2013-2014学年湖北省黄冈市中考模拟考试数学试卷A(解析版) 题型:解答题
有四部不同的电影,分别记为A, B, C, D.
(1)若甲从中随机选择一部观看,则恰好是电影A的概率是 ;
(2)若甲从中随机选择一部观看,乙也从中随机选择一部观看,求甲、乙两人选择同一部电影的概率.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省鄂州市九年级4月调研考试数学试卷(解析版) 题型:选择题
如图,抛物线y1=a(x+2)2-3与 交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B、C,则以下结论:①无论x取何值,y2总是正数;②a=1;③当x=0时,y2-y1=4;④2AB=3AC.其中正确的是( )
交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B、C,则以下结论:①无论x取何值,y2总是正数;②a=1;③当x=0时,y2-y1=4;④2AB=3AC.其中正确的是( )

A.①② B.②③ C.③④ D.①④
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省襄阳市襄州区九年级中考适应性测试数学试卷(解析版) 题型:选择题
如图,直线y=x+a-5与双曲线y=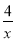 交于A,B两点,则当线段AB的长度取最小值时, a的值为( ).
交于A,B两点,则当线段AB的长度取最小值时, a的值为( ).
A.0 B.1 C.2 D.5

查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省十堰市九年级4月调研考试数学试卷(解析版) 题型:解答题
某企业向阳光小学赠送300个学生书包.现用A,B两种不同的包装箱进行包装,单独用B型包装箱比单独用A型包装箱少用10个,已知每个B型包装箱比每个A型包装箱多装5个书包.求A,B两种包装箱各能装书包多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com