
����Ŀ��̽��n��n�������ζ��Ӱ���(n�Ƕ��Ӱ�ÿ���ϵĶ�����,ÿ�������ڶ��Ӽ�ľ���Ϊ1),�������������������õ��IJ�ͬ����ֵ���߶�����:
��n=2ʱ,���Ӱ���������ͬ�߶εij���ֵֻ��1��![]() �����Բ�ͬ����ֵ���߶�ֻ��2��,����S��ʾ��ͬ����ֵ���߶�����,��S=2;
�����Բ�ͬ����ֵ���߶�ֻ��2��,����S��ʾ��ͬ����ֵ���߶�����,��S=2;
��n=3ʱ,���Ӱ���������ͬ�߶εij���ֵֻ��1, ![]() ��2,
��2, ![]() ��2
��2![]() ����,��n=2ʱ������3��,��S=2+3=5.
����,��n=2ʱ������3��,��S=2+3=5.
(1)�۲�ͼ��,��д�±�:
������(n��n) | Sֵ |
2��2 | 2 |
3��3 | 2+3 |
4��4 | 2+3+��____�� |
5��5 | ��________�� |
(2)д��(n-1)��(n-1)��n��n���������Ӱ���,��ͬ����ֵ���߶�����֮��Ĺ�ϵ;(��ʽ�ӻ����Ա�������).
(3)��n��n�Ķ��Ӱ�,д����n��ʾS�Ĵ���ʽ.
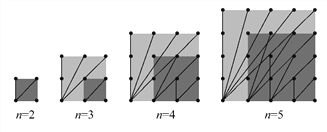
���𰸡� 4 2+3+4+5(��14)
�������������������1��������Ϊ2��2ʱ�����в�ͬ���߶�2����
������Ϊ3��3ʱ�����в�ͬ���߶�2+3����
������Ϊ4��4ʱ�����в�ͬ���߶�2+3+4����
��ô������Ϊ5��5ʱ�����в�ͬ���߶�2+3+4+5����
��2��������Ϊ��n-1������n-1��ʱ�����в�ͬ���߶�2+3+4+5+��+��n-1������������Ϊn��nʱ�����в�ͬ���߶�2+3+4+5+��+��n-1��+n��������ֲ�ͬ���ȵ��߶�����������n�֣�
��3��������Ϊn��nʱ�����в�ͬ���߶�Ӧ��2��ʼ�ӣ��ӵ�n��
���������(1)4��2+3+4+5(��14)
(2)��n��n�Ķ��Ӱ��(n-1)��(n-1)�Ķ��Ӱ��в�ͬ���ȵ��߶�����������n�ֻ�ڷֱ���a,b��ʾn��n��(n-1)��(n-1)�Ķ��Ӱ��в�ͬ���ȵ��߶�����,��a=b+n.
(3)S=2+3+4+��+n=![]() ��(n-1)=
��(n-1)= ![]() .
.


 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OΪԲ�ģ��ʵ���Ϊ�뾶��������x���ڵ�M����y���ڵ�N���ٷֱ��Ե�M��NΪԲ�ģ�����![]() MN�ij�Ϊ�뾶�����������ڵڶ������ڵ�P������P������Ϊ��2a��b+1������a��b��������ϵΪ������
MN�ij�Ϊ�뾶�����������ڵڶ������ڵ�P������P������Ϊ��2a��b+1������a��b��������ϵΪ������
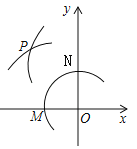
A. a=b B. 2a��b=1 C. 2a+b=��1 D. 2a+b=1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0����ͼ����ͼ�����������ĸ����ۣ���4ac��b2��0����4a+c��2b����3b+2c��0����m��am+b��+b��a��m�٩�1����������ȷ���۵ĸ����ǣ�����
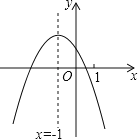
A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD�ĶԽ���![]() ��
��![]() ���ڵ�
���ڵ�![]() ��˳������ABCD�����е�õ���һ���µ��ı��Σ�������������ĸ������е�һ����������
��˳������ABCD�����е�õ���һ���µ��ı��Σ�������������ĸ������е�һ����������![]() ��
��![]() ����
����![]() ����
����![]() ����
����![]() ������ʹ����µ��ı��γ�Ϊ���Σ���ô���������������ǣ���
������ʹ����µ��ı��γ�Ϊ���Σ���ô���������������ǣ���

A. 1����B. 2����
C. 3����D. 4����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���![]() �������һ��ֱ�����������У��ٶ��������е�·�̼����������������е�·�̼������������еĸ���·�̣���λ��
�������һ��ֱ�����������У��ٶ��������е�·�̼����������������е�·�̼������������еĸ���·�̣���λ��![]() ������Ϊ��
��������![]() .
.
��1��С�������й�������![]() ����Զ�ľ����Ƕ��٣�
����Զ�ľ����Ƕ��٣�
��2��С����������![]() ���Զ��
���Զ��
��3�����С������![]() �ͽ�����һ��֥�飬��ôС��һ���ɵõ�������֥�飿
�ͽ�����һ��֥�飬��ôС��һ���ɵõ�������֥�飿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ,����ÿ��С�����εı߳�Ϊ1����λ����.
(1)����ABC����ƽ��2����λ����,����ƽ�ƺ�ġ�A1B1C1,��д����A1B1C1�����������.
(2)������ABC�Ƶ�(-1,0)˳ʱ����ת180���õ���A2B2C2,��д����A2B2C2�����������.
(3)�۲��A1B1C1�͡�A2B2C2,�����Ƿ����ij������ĶԳ�?����,��д���Գ����ĵ�����;������,˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ�ķ���ֽ�У�ÿ��С�����εı߳�Ϊ1��ÿ��С�����εĶ��㶼������㣮��������������ͼ��������������Ǧ�������ڣ�

��1������C��AB�Ĵ��ߣ�����������������E��
��2������C��AB��ƽ����CF�������ƽ�����������F��
��3��ֱ��CE��ֱ��CF��λ�ù�ϵ���� ����
��4������AC��BC����������ABC������� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���ֽ���ʽ��xy2��2xy+x
��2��������ʽ��3x��![]() ��1��1��������λ��Ϊ���������������У���x��ȡֵ��Χ��
��1��1��������λ��Ϊ���������������У���x��ȡֵ��Χ��
��3������![]()
��4���Ȼ�������ֵ![]() ������x��
������x��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������ֱ���������ߣ�![]() ���룩�������ĸ߶�
���룩�������ĸ߶�![]() ���ף����ù�ʽ
���ף����ù�ʽ![]() .
.
��1����������ʱ����ĸ߶�Ϊ20�ף�
��2��С��ͬѧ˵��������߶Ȳ����ܴﵽ21�ף�������Ϊ��˵�ö�����˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com