
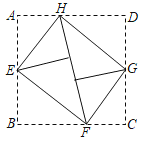
【题目】如图,将矩形ABCD的四个角向内折起,恰好拼成一个既无缝隙又不重叠的四边形EFGH,若EH=4,EF=5,那么线段AD与AB的比等于_____.
【答案】![]() .
.
【解析】
先根据图形翻折的性质可得到四边形EFGH是矩形,由“AAS”可证Rt△AHE≌Rt△CFG,可得AH=CF=FN,再由勾股定理及直角三角形的面积公式求出AD,AB的长,即可求解.
如图:
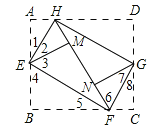
由折叠的性质可得:∠1=∠2,∠3=∠4,AE=EM=BE,DH=HN,CF=FN,
∴∠2+∠3=90°,
∴∠HEF=90°,
同理四边形EFGH的其它内角都是90°,
∴四边形EFGH是矩形.
∴EH=FG;
又∵∠1+∠4=90°,∠4+∠5=90°,
∴∠1=∠5,
同理∠5=∠7=∠8,
∴∠1=∠8,
∴Rt△AHE≌Rt△CFG(AAS),
∴AH=CF=FN,
又∵HD=HN,
∴AD=HF,
在Rt△HEF中,EH=4,EF=5,根据勾股定理得HF=![]() =
=![]() =AD,
=AD,
∵S△EFH=![]() ×EF×EH=
×EF×EH=![]() ×HF×EM,
×HF×EM,
∴EM=![]() ,
,
∴AB=2AE=2EM=![]() ,
,
∴AD:AB=41:40=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 的图象经过
的图象经过![]() 和
和![]() 两点,且与
两点,且与![]() 轴交于
轴交于![]() ,直线
,直线![]() 是抛物线的对称轴,过点
是抛物线的对称轴,过点![]() 的直线
的直线![]() 与直线相交于点
与直线相交于点![]() ,且点
,且点![]() 在第一象限.
在第一象限.

(1)求该抛物线的解析式;
(2)若直线![]() 和直线
和直线![]() 、
、![]() 轴围成的三角形面积为6,求此直线的解析式;
轴围成的三角形面积为6,求此直线的解析式;
(3)点![]() 在抛物线的对称轴上,
在抛物线的对称轴上,![]() 与直线
与直线![]() 和
和![]() 轴都相切,求点
轴都相切,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支持国家南水北调工程建设,小王家由原来养殖户变为种植户,经市场调查得知,当种植樱桃的面积x不超过15亩时,每亩可获得利润y=1900元;超过15亩时,每亩获得利润y(元)与种植面积x(亩)之间的函数关系如下表(为所学过的一次函数,反比例函数或二次函数中的一种)
x(亩) | 20 | 25 | 30 | 35 |
y(元) | 1800 | 1700 | 1600 | 1500 |
(1)请求出种植樱桃的面积超过15亩时每亩获得利润y与x的函数关系式;
(2)如果小王家计划承包荒山种植樱桃,受条件限制种植樱桃面积x不超过50亩,设小王家种植x亩樱桃所获得的总利润为W元,求小王家承包多少亩荒山获得的总利润最大,并求总利润W(元)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某无人机兴趣小组在操场上开展活动(如图),此时无人机在离地面30米的D处,无人机测得操控者A的俯角为37°,测得点C处的俯角为45°.又经过人工测量操控者A和教学楼BC距离为57米,求教学楼BC的高度.(注:点A,B,C,D都在同一平面上.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线W的图象与x轴交于A、O两点,顶点为点B(﹣1,﹣1).
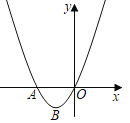
(1)求抛物线W的表达式;
(2)将抛物线W绕点A旋转180°得到抛物线V,使抛物线V的顶点为E,试通过计算判断抛物线V是否过点B;
(3)在抛物线W或V的图象上是否存在点D,使S△EBD=S△EBO?若存在,请求出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
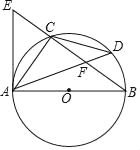
【题目】如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,点D是![]() 上的一点,且
上的一点,且![]() ,连接AD交BC于点F,过点A作⊙O的切线AE交BC的延长线于点E.
,连接AD交BC于点F,过点A作⊙O的切线AE交BC的延长线于点E.
(1)求证:CF=CE;
(2)若AD=8,AC=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某植物园有一块足够大的空地,其中有一堵长为a米的墙,现准备用20米的篱笆围两间矩形花圃,中间用篱笆隔开.小俊设计了如图甲和乙的两种方案:
方案甲中AD的长不超过墙长;方案乙中AD的长大于墙长.
(1)若a=6.
①按图甲的方案,要围成面积为25平方米的花圃,则AD的长是多少米?
②按图乙的方案,能围成的矩形花圃的最大面积是多少?
(2)若0<a<6.5,哪种方案能围成面积最大的矩形花圃?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com