
【题目】计算或化简:
(1)计算:(-2)×![]() ÷(-
÷(-![]() )×4+(- 2)3;
)×4+(- 2)3;
(2)计算:(-1)2019-(1-![]() )÷3×[3-(-3)2];
)÷3×[3-(-3)2];
(3)化简:4a2- 2(a2- b2)- 3(a2+ b2).
科目:初中数学 来源: 题型:
【题目】在四边形OABC中,AB∥OC,∠OAB=90°, ∠OCB=60°,AB=2,OA=2![]() .
.
(1)如图①,连接OB,请直接写出OB的长度;
(2)如图②,过点O作OH⊥BC于点H.动点P从点H出发,沿线段HO向点O运动,动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,设点P运动的时间为t秒,△OPQ的面积为S(平方单位).
①求S与t之间的函数关系式;
②设PQ与OB交于点M,当△OPM为等腰三角形时,试求出△OPQ的面积S的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3![]() .其中正确的结论有( )
.其中正确的结论有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
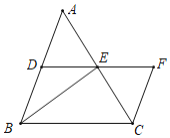
【题目】如图,在△ABC中,点D,E分别是边AB,AC的中点,过点C作CF∥AB交DE的延长线于点F,连接BE.
(1)求证:四边形BCFD是平行四边形.
(2)当AB=BC时,若BD=2,BE=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图一条抛物线![]() (a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.

(1)“抛物线三角形”一定是_______________三角形;
(2)若抛物线y=-x2+bx(b>0)的“抛物线三角形”是等腰直角三角形,求b的值;
(3)如图,△OAB是抛物线y=-x2+b′x(b′>0)的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
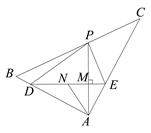
【题目】△ABC中,AB=6,AC=8,BC=10,P为BC边上一动点,过线段AP上的点M作DE⊥AP,交边AB于点D,交边AC于点E,点N为DE中点,若四边形ADPE的面积为18,则AN的最大值=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙二人用4张扑克牌(分别是红桃2,红桃3,黑桃4,方片5)玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先取一张,取出的牌不放回,乙从剩余的牌中取一张.
(1)设![]() 、
、![]() 分别表示甲、乙取出的牌面上的数字,写出
分别表示甲、乙取出的牌面上的数字,写出![]() 的所有结果;
的所有结果;
(2)若甲取到红桃3,则乙取出的牌面数字比3大的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,点
两点,点![]() 是
是![]() 轴上一动点,要使点
轴上一动点,要使点![]() 关于直线
关于直线![]() 的对称点刚好落在
的对称点刚好落在![]() 轴上,则此时点
轴上,则此时点![]() 的坐标是( )
的坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个三位数![]() ,如果
,如果![]() 满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为
满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为![]() .例如
.例如![]() ,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以
,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以![]() .
.
(1)计算:![]() 和
和![]() ;
;
(2)若![]() 是“相异数”,证明:
是“相异数”,证明:![]() 等于
等于![]() 的各数位上的数字之和.
的各数位上的数字之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com