
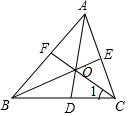
 如图,△ABC的三条角平分线AD、BE、CF交于点O.
如图,△ABC的三条角平分线AD、BE、CF交于点O.分析 (1)利用角平分线的定义,得出∠2=$\frac{1}{2}$∠ABC,∠3=$\frac{1}{2}$∠BAC,∠1=$\frac{1}{2}$∠ACB,再根据∠AOE是△AOB的外角,得出∠AOE=∠2+∠3,据此进行计算,即可得出AOE+∠1=90°;
(2)利用三角形的内角和定理,以及角平分线的定义,用∠ACB表示出∠AOE,则∠BOD即可得到,然后在直角△OCH中,利用直角三角形的两个内角互余以及角平分线的定义,即可利用∠ACB表示出∠COH,从而证得结论.
解答 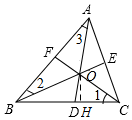 解:(1)∠AOE和∠1之间的关系:∠AOE+∠1=90°.
解:(1)∠AOE和∠1之间的关系:∠AOE+∠1=90°.
理由:∵AD、BE、CF都是△ABC的角平分线,
∴∠2=$\frac{1}{2}$∠ABC,∠3=$\frac{1}{2}$∠BAC,∠1=$\frac{1}{2}$∠ACB,
∵∠AOE是△AOB的外角,
∴∠AOE=∠2+∠3
=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠BAC
=$\frac{1}{2}$(∠ABC+∠BAC)
=$\frac{1}{2}$(180°-∠ACB)
=90°-$\frac{1}{2}$∠ACB
=90°-∠1,
∴∠AOE+∠1=90°;
(2)证明:过点O作BC的垂线段,交BC于点H,
∵∠AEO=∠EBC+∠ACB=$\frac{1}{2}$∠ABC+∠ACB,
∴∠AOE=180°-(∠DAC+∠AEO)
=180°-[$\frac{1}{2}$∠BAC+$\frac{1}{2}$∠ABC+∠ACB]
=180°-[$\frac{1}{2}$(∠BAC+∠ABC)+∠ACB]
=180°-[$\frac{1}{2}$(180°-∠ACB)+∠ACB]
=180°-[90°+$\frac{1}{2}$∠ACB]
=90°-$\frac{1}{2}$∠ACB,
∴∠BOD=∠AOE=90°-$\frac{1}{2}$∠ACB,
又∵在Rt△OCH中,∠COH=90°-∠OCD=90°-$\frac{1}{2}$∠ACB,
∴∠BOD=∠COH.
点评 本题主要考查了角平分线的定义,三角形的外角的性质以及三角形的内角和定理,解题时注意运用:三角形内角和是180°,三角形的一个外角等于和它不相邻的两个内角的和.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是某住宅的平面结构示意图,图中标注了有关尺寸(墙体厚度勿略不计,单位:m).
如图是某住宅的平面结构示意图,图中标注了有关尺寸(墙体厚度勿略不计,单位:m).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
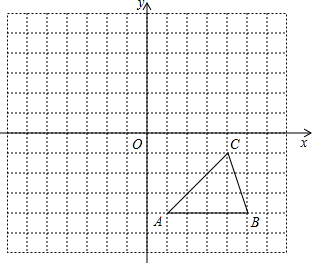 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com