
【题目】如图,在四边形ABCD中,AD∥BC,AB=BC=6,∠B=60°,∠D=90°,连结AC.动点P从点B出发,沿BC以每秒1个单位的速度向终点C运动(点P不与点B、C重合).过点P作PQ⊥BC交AB或AC于点Q,以PQ为斜边作Rt△PQR,使PR∥AB.设点P的运动时间为t秒.

(1)当点Q在线段AB上时,求线段PQ的长.(用含t的代数式表示)
(2)当点R落在线段AC上时,求t的值.
(3)设△PQR与△ABC重叠部分图形的面积为S平方单位,求S与t之间的函数关系式.
(4)当点R到C、D两点的距离相等时,直接写出t的值.
【答案】(1)![]() t(0<t≤3);(2)
t(0<t≤3);(2)![]() s;(3)当0<t≤
s;(3)当0<t≤![]() 时,S==
时,S==![]() t2;当
t2;当![]() <t≤3时,S=﹣
<t≤3时,S=﹣![]() t2+15
t2+15![]() t﹣18
t﹣18![]() ;当3<t<6时,S=﹣
;当3<t<6时,S=﹣![]() t2﹣3
t2﹣3![]() t+9
t+9![]() ;(4)2s或4s.
;(4)2s或4s.
【解析】试题分析:(1)Rt△PQB中利用解直角三角形易求出线段PQ的长。
(2)当R落在AC上时,易知PC=RC=PQ,在Rt△PQR中,利用解直角三角形求出PR=32t,由BP+PC=6,建立方程求出t的值。
(3)分三种情况进行讨论:如图3中.当0<t≤![]() 时,重叠部分是△PQR.根据三角形的面积公式,可求出S与t之间的函数关系式;如图4中,当
时,重叠部分是△PQR.根据三角形的面积公式,可求出S与t之间的函数关系式;如图4中,当 ![]() <t≤3时,重叠部分是四边形PMNQ,根据S=S△PQR﹣S△RMN即可求出结果;如图5中,当3<t<6时,重叠部分是△PQM.则S=
<t≤3时,重叠部分是四边形PMNQ,根据S=S△PQR﹣S△RMN即可求出结果;如图5中,当3<t<6时,重叠部分是△PQM.则S= ![]() S△PQC , 即可求出S与t之间的函数关系式。
S△PQC , 即可求出S与t之间的函数关系式。
(4)根据两种情况在图3和图5中,根据点R到C、D两点的距离相等建立方程求解即可。
(1)解:如图1中,

当点Q在线段AB上时,BP=t,
在Rt△PQB中,∵∠BPQ=90°,∠B=60°,
∴PQ=BPtan60°= ![]() t(0<t≤3)
t(0<t≤3)
(2)解:如图2中,

当R落在AC上时,易知PC=RC=PQ,
在Rt△PQR中,∵∠PRQ=90°,PQ= ![]() t,∠PQR=60°,
t,∠PQR=60°,
∴PR=PQsin60°= ![]() t,
t,
由BP+PC=6可得,t+ ![]() t=6,
t=6,
解得t= ![]() s
s
(3)解:如图3中.当0<t≤ ![]() 时,重叠部分是△PQR.
时,重叠部分是△PQR.
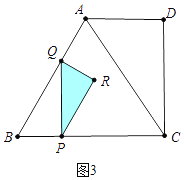
S= ![]() QRPR=
QRPR= ![]()
![]() t
t ![]() t=
t= ![]() t2 .
t2 .
如图4中,当 ![]() <t≤3时,重叠部分是四边形PMNQ.
<t≤3时,重叠部分是四边形PMNQ.
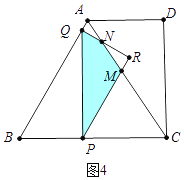
S=S△PQR﹣S△RMN= ![]() t2﹣
t2﹣ ![]() [
[ ![]() t﹣(6﹣t)]
t﹣(6﹣t)] ![]() [
[ ![]() t﹣(6﹣t)]=﹣
t﹣(6﹣t)]=﹣ ![]() t2+15
t2+15 ![]() t﹣18
t﹣18 ![]() .
.
如图5中,当3<t<6时,重叠部分是△PQM.
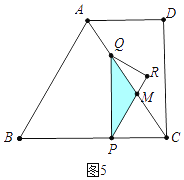
S= ![]() S△PQC=
S△PQC= ![]()
![]() (6﹣t)
(6﹣t) ![]() (6﹣t)=
(6﹣t)= ![]() t2﹣3
t2﹣3 ![]() t+9
t+9 ![]()
(4)解:在图3中,点R到C、D两点的距离相等时,则有 ![]() tsin60°=
tsin60°= ![]() ×6×
×6× ![]() ,解得t=2.
,解得t=2.
在图5中,点R到C、D两点的距离相等时,则有 ![]() (6﹣t)
(6﹣t) ![]() =
= ![]() 6
6 ![]() ,解得t=4.
,解得t=4.
综上所述,t=2s或4s时,点R到C、D两点的距离相等


科目:初中数学 来源: 题型:
【题目】甲、乙两商场以同样价格出售同样的商品:并且又各自推出不同的优惠方案,在甲商场累计购物超过100元后,超出100元的部分按![]() 收费;在乙商场累计购物超过50元后,超出50元的部分按
收费;在乙商场累计购物超过50元后,超出50元的部分按![]() 收费.顾客到哪家商场购物花费少?
收费.顾客到哪家商场购物花费少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有甲、乙两个空调安装队分别为A、B两个公司安装空调,甲安装队为A公司安装66台空调,乙安装队为B公司安装60台空调,甲、乙两队安装空调所用的总时间相同.已知甲队比乙队平均每天多安装2台空调,求甲、乙两个安装队平均每天各安装空调的台数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是正
是正![]() 内一点,
内一点,![]() ,
,![]() ,
,![]() ,将线段
,将线段![]() 以点
以点![]() 为旋转中心逆时针旋转
为旋转中心逆时针旋转![]() 得到线段
得到线段![]() ,下列结论:①
,下列结论:①![]() 可以由
可以由![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到;②点
得到;②点![]() 与点
与点![]() 的距离为8;③
的距离为8;③![]() ;④
;④![]() ;其中正确的结论是( )
;其中正确的结论是( )

A.①②③B.①③④C.②③④D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”n的各个数位上的数字之和记为F(n).例如n=135时,F(135)=1+3+5=9.
(1)对于“相异数”n,若F(n)=6,请你写出一个n的值;
(2)若a,b都是“相异数”,其中a=100x+12,b=350+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k=![]() ,当F(a)+F(b)=18时,求k的最小值.
,当F(a)+F(b)=18时,求k的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
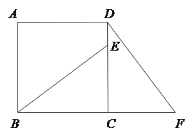
【题目】已知:如图,在正方形ABCD中,E是CD边上的一点,F为BC延长线上一点,且CE=CF.
(1)求证:△BEC≌△DFC;
(2)如果BC+DF=9,CF=3,求正方形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路MN和公路PQ在点O处交汇,∠QON=30°,在点A处有一栋居民楼,AO=320m,如果火车行驶时,周围200m以内会受到噪音的影响,那么火车在铁路MN上沿ON方向行驶时.
(1)居民楼是否会受到噪音的影响?请说明理由;
(2)如果行驶的速度为72km/h,居民楼受噪音影响的时间为多少秒?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自从在龟兔赛跑中大胜兔子后,乌龟便成了体育界的名人,又是广告,又是讲演,活动不断.可蚂蚁偏偏不服气,向乌龟下了挑战书,我们来看:
乌龟先生:
本月12日下午两时整,我与你进行长跑比赛,兔子先生做裁判,从小柳树开始跑到相距6米的大柳树下,比赛枪声响后,先到者是冠军.
蚂蚁
4月9日
比赛结束后,蚂蚁并没有取胜.已知在此次比赛中,乌龟的速度是蚂蚁的2倍,乌龟提前1分钟到达.请你利用所学分式方程的知识,帮他们算算各自的速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com