
【题目】如图:在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.
(1)MN=AM+BN成立吗?为什么?
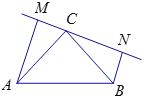
(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由.

【答案】(1)MN=AM+BN成立,理由见解析;(2)MN=BNAM,理由见解析.
【解析】
(1)利用同角的余角相等证明∠MAC=∠NCB,由∠AMC=∠CNB=90°,AC=BC,可证△AMC≌△CNB,从而有AM=CN,MC=BN,即可得出结论;
(2)类似于(1)的方法,证明△AMC≌△CNB,从而有AM=CN,MC=BN,可推出AM、BN与MN之间的数量关系.
解:(1)MN=AM+BN成立;
理由:∵AM⊥MN,BN⊥MN,
∴∠AMC=∠CNB=90°,
∵∠ACB=90°,
∴∠MAC+∠ACM=90°,∠NCB+∠ACM=90°,
∴∠MAC=∠NCB,
在△AMC和△CNB中,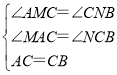 ,
,
∴△AMC≌△CNB(AAS),
∴AM=CN,MC=BN,
∵MN=CN+MC,
∴MN=AM+BN;
(2)MN=BNAM.
理由:∵AM⊥MN,BN⊥MN,
∴∠AMC=∠CNB=90°,
∵∠ACB=90°,
∴∠MAC+∠ACM=90°,∠NCB+∠ACM=90°,
∴∠MAC=∠NCB,
在△AMC和△CNB中,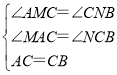 ,
,
∴△AMC≌△CNB(AAS),
∴AM=CN,MC=BN,
∵MN=MCCN,
∴MN=BNAM.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】图,反比例函数![]() 的图象经过点A(1,4),直线y=2x+b(b≠0)与双曲线
的图象经过点A(1,4),直线y=2x+b(b≠0)与双曲线![]() 在第一、三象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点.(1)求k的值;(2)当b=-3时,求△OCD的面积;
在第一、三象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点.(1)求k的值;(2)当b=-3时,求△OCD的面积;
(3)连接OQ,是否存在实数b,使得S△ODQ=S△OCD?若存在,请求出b的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正确结论的序号是 .
.其中正确结论的序号是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连接EF与边CD相交于点G,连接BE与对角线AC相交于点H, AE=CF,BE=EG。

(1)求证:EF//AC;
(2)求∠BEF大小;
(3)求证: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D,E分别是AB,AC上的点,BE与CD交与点O,给出下列四个条件:①∠DBO=∠ECO,②∠BDO=∠CEO,③BD=CE,④OB=OC.
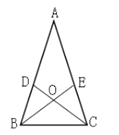
(1)从上述四个条件中,任选两个为条件,可以判定△ABC是等腰三角形?写出所有可能的情况.
(2)选择(1)中的某一种情形,进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、D、B、E四点在同一条直线上,AD=BE,BC∥EF,BC=EF.

(1)求证:AC=DF;
(2)若CD为∠ACB的平分线,∠A=25°,∠E=71°,求∠CDF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】11月5日晚在西昌卫星发射中心成功以“一箭双星”方式发射第24颗、第25颗北斗导航卫星,“中国的北斗,世界的北斗”,北斗卫星系统是由中国自主研发的全球领先的卫星导航系统,这套天罗地网在不久的将来会造福人类、服务全球.第三期北斗系统总项目预算国拨总投资为240亿元,分技术、基建、设备三个项目投资,基建项目投资占技术项目投资的![]() ,设备项目投资比技术项目投资少40%,由于物价的上涨,总项目的实际总投资随之增长,基建项目投资的增长率是技术项目投资增长率的2.5倍,设备项目投资的增长率达到基建项目投资增长率的2倍.
,设备项目投资比技术项目投资少40%,由于物价的上涨,总项目的实际总投资随之增长,基建项目投资的增长率是技术项目投资增长率的2.5倍,设备项目投资的增长率达到基建项目投资增长率的2倍.
(1)三个项目的预算投资分别是多少亿元?
(2)由于技术工人齐心协力,整套导航系统提前半年交付使用,导航系统每月可供1000万台导航设备使用,每台导航设备的平均月使用费为40元,这样,可将提前半年使用的收益的70%用于该项目的实际投资,减少了国拨投资,使预算国拨总投资减少的百分率与技术项目投资的增长率相同,问第三期北斗系统工程的实际总投资是多少亿元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com